Понятие простой динамической системы

Обзор систем моделирования динамических систем

Математическое моделирование

По А. А. Ляпунову моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

· находящаяся в некотором объективном соответствии с познаваемым объектом;

· способная замещать его в определенных отношениях;

· дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.[1]

По учебнику Советова и Яковлева [2]:

1) Модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

2) «Моделированием называется замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели.

3) Под математическим моделированием понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.

В общем случае математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.

Понятие простой динамической системы

Под “динамической системой в широком смысле” понимается объект, функционирующий в непрерывном времени, непрерывно наблюдаемый и изменяющий свое состояние под воздействием внешних и внутренних причин.

Под простейшей динамической системой обычно понимается система, поведение которой задается совокупностью обыкновенных дифференциальных уравнений в форме Коши с достаточно гладкими правыми частями, обеспечивающими существование и единственность решения:

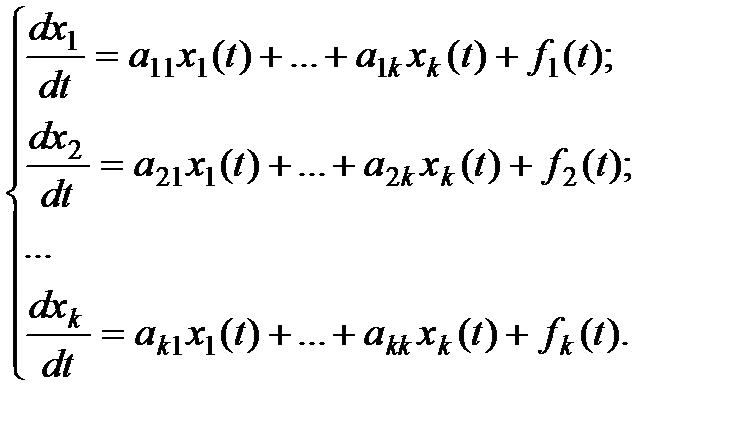(1.1)

где:

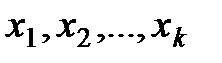- неизвестные координаты системы;

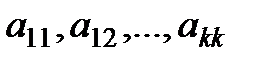- постоянные коэффициенты;

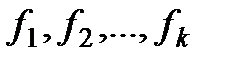– функции, зависящие только от параметра t.

Примерами объектов, поведение которых может быть описано системой дифференциальных уравнений (1.1), является, например, тело, брошенное под углом к горизонту, или известный из школьного задачника бассейн с двумя трубами, через которые вливается и выливается вода. Решение систем уравнений в форме Коши, разрешенных относительно первых производных, - традиционная численная задача. Разработанные в последние годы программные реализации численных методов не только обеспечивают заданные требования к погрешности решения, но стараются самостоятельно определить тип (вычислительную сложность) решаемой задачи.

Более сложной является модель, представленная системой обыкновенных дифференциальных уравнений в форме Коши и нелинейных алгебраических уравнений, сопровождаемая набором вспомогательных формул:

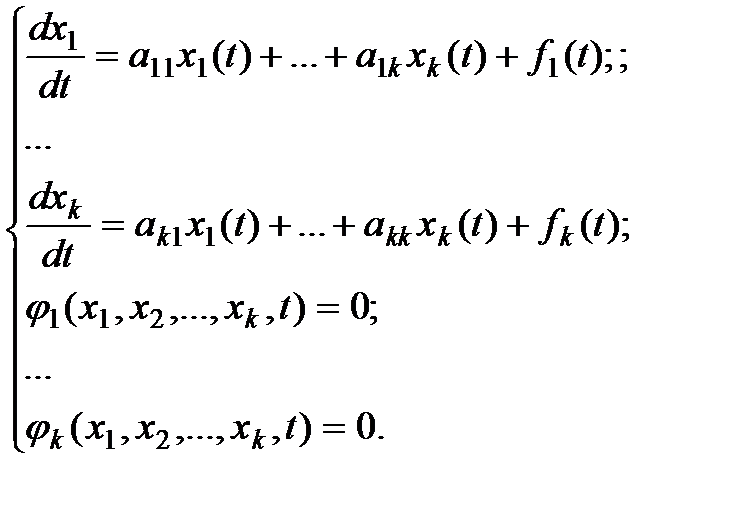(1.2)

где:

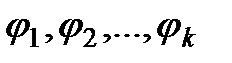- линейные (нелинейные) уравнения, связывающие координаты системы.

Задача численного построения фазовой траектории такой системы значительно сложнее, но если совокупность нелинейных уравнений однозначно разрешима в каждой временной точке, и правые части дифференциальных уравнений достаточно гладкие, то она в основном также вполне успешно решается. Предварительная подготовка для численного решения в данном случае минимальна: нужно проверить равно ли число уравнений числу неизвестных, проверить согласованность начальных условий и провести сортировку формул в правильном порядке (для замены их операторами присваивания). Такую систему будем называть простой динамической системой.

Если бы все моделируемые системы укладывались бы в формализацию простой динамической системы, моделирование было бы достаточно простым (следует помнить, что конкретные случаи простых динамических систем могут породить массу вычислительных проблем). К сожалению, большинство технических и природных систем являются более сложными. Выделяют структурную и поведенческую сложность моделируемых объектов.