Соединение фаз нагрузки по схеме «звезда»

Концы фаз нагрузки x, y и z в этом случае объединяются в один узел, обозначаемый «n» и, как и на стороне генератора, называемый нулевымили нейтральным (рис. 9).

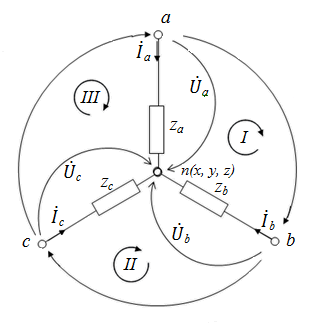
Рис. 9.

Фазы нагрузки при этом обозначаются буквами их начал, т.е. «a», «b» и «c».

В соответствии с введенными ранее определениями фазными напряжениями здесь являются 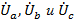, а фазными токами соответственно 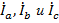, а векторы 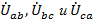представляют линейные напряжения.

По второму закону Кирхгофа для внешнего и трех (I, II, III) внутренних контуров схемы (рис. 9) получаем соотношения между фазными и линейными напряжениями на нагрузке, а именно

,

,

,

.

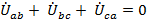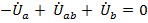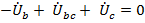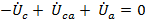Как видно, эти соотношения по форме полностью совпадают с соответствующими формулами связи на стороне генератора и лежат в основе расчетов и построения векторных диаграмм. Понятно, что на векторной диаграмме каждая тройка входящих в приведенные уравнения векторов образует замкнутый треугольник (рис. 10).

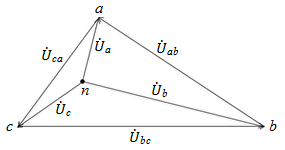
Рис. 10.

Линейные напряжения 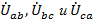образуют треугольник abc, вершины которого, как и на генераторе обозначаются буквами начал соответствующих фаз. В случае симметричной системы на стороне нагрузки этот треугольник, как и на стороне генератора, будет равносторонним. В случае несимметричной нагрузки, как будет показано, это будет произвольный треугольник со смещенным от центра положением нейтральной точки «n» (рис. 10). Точка «n» при этом оказывается общей вершиной для любых двух фазных (например, 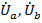) и соответствующего линейного (в этом случае 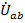) напряжения.

Это – разные треугольники с условно произвольным положением нейтральной точки «n». Теоретически она может оказаться даже вне треугольника abc.

Это означает, что соотношения между фазными и линейными напряжениями, полученные при анализе симметричной системы напряжений на стороне генератора, а именно 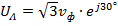, при несимметричных нагрузках не действуют.

Только при симметричных нагрузках, как будет показано, векторная диаграмма напряжений будет представлять из себя равносторонний треугольник линейных напряжений и равновеликую трехлучевую звезду фазных. Только в случае симметричной нагрузки линейные и фазные напряжения одинаковы между собою по величине и смещены друг относительно друга по фазе на 120° (рис. 11). Линейные напряжения в этом случае опережают фазные на угол 30º.

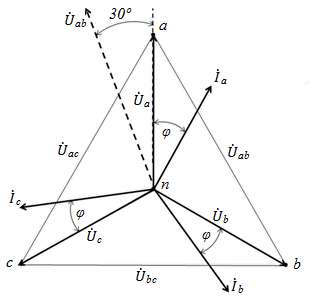
Рис. 11

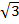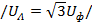Нейтральная точка «n» в этом случае расположена в центре равностороннего треугольника, линейные напряжения по модулю больше фазных в раз , а по фазе линейное напряжение опережает соответствующее фазное на угол 30°. Соотношение между фазным напряжением и соответствующим фазным током формируется правилами расчета и анализа однофазных приемников. Например, при симметричной нагрузке индуктивного характера векторы фазных токов на векторной диаграмме напряжений располагаются так, как показано на рис. 11. Токи в каждой фазе одинаковы по величине и отстают от соответствующего фазного напряжения на один и тот же угол φ.

В случае несимметричной нагрузки и, как следствие, несимметричной системы напряжений величины токов 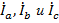и сдвиги по фазе относительно фазных напряжений 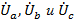отличаются друг от друга, совпадая, отставая или опережая по фазе соответствующие напряжения.