Сферическая и хроматическая аберрация. Обманы зрения

Сферическая аберрация. 1) Кусок картона с отверстием. 2) Книга.

Как было выяснено (§ 35, 1 и 6), сферическая аберрация создает неясность изображения, устранимую с помощью диафрагмы. Подобное явление можно обнаружить в глазе. Если смотреть на печать в книге на близком расстоянии, то изображение является совершенно не ясным; если теперь перед глазом поместить кусок картона с небольшим отверстием (d= 1—2 мм), то изображение становится более или менее отчетливым.

Сферической аберрацией объясняется явление иррадиации, заключающейся в том, что черные предметы на белом фоне кажутся уменьшенными, а белые на черном—увеличенными (рис. 387) вследствие расплывчатости границ изображения белого предмета. Белые кружки на черном фоне (рис. 388) при рассматривании издали принимают форму шестиугольников.

Рис. 387. Рисунки для наблюдения иррадиации

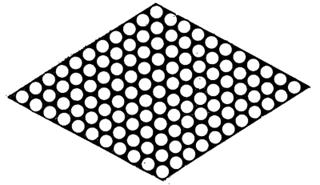
Рис. 388. Рисунки для наблюдения иррадиации

Узкий серп Луны кажется имеющим больший радиус, чем остальная часть Луны, освещенная пепельным светом (отраженным от Земли). Это явление можно показать на экране при помощи диапозитива (рис. 389), где круглое отверстие закрывают подвижной полупрозрачной ширмой.

Рис. 389. Диапозитив для демонстрации иррадиации лунного серпа

Хроматическая аберрация. 1) Картон. 2) Булавка. Эта аберрация сказывается в окраске краев изображения (§ 35, 2) видимого глазом, в красный или в синий цвет. Производя опыт Шейнера (§39, 1), эту окраску легко заметить. Когда два изображения булавки приближаются почти вплотную, то промежуток между ними приобретает окраску, которая становится особенно яркой, когда оба изображения частично налягут друг на друга. При этом цвет общей полоски обоих изображений — красный, когда булавка расположена ближе, к глазу, нежели ближняя точка, и цвет — синий, когда булавка стоит дальше ближней точки (рис. 385).

Обманы зрения. Специальные таблицы или диапозитивы. Глаз легко поддается обманам зрения, когда приходится сравнивать на-глаз размеры предметов или их расстояние от глаза, или взаимное расположение прямых линий.

Возникновение ошибки в оценке размеров зависит от обстановки, окружающей сравниваемые предметы; протяжение в пустом пространстве кажется большим, чем такое же расстояние в пространстве, густо заполненном предметами. На рис. 391 приведено несколько обманов зрения: 1 — прямая CD кажется длиннее, чем AB; 2 — квадрат из горизонтальных линий кажется выше, чем квадрат из вертикальных; 3 — диагональ AB кажется длиннее ВС; 4 — кружок кажется тем больше, чем ближе он лежит к вершине угла. Прямая линия, пересекающая наклонно несколько параллельных прямых, кажется ломаной (рис. 391, 5).

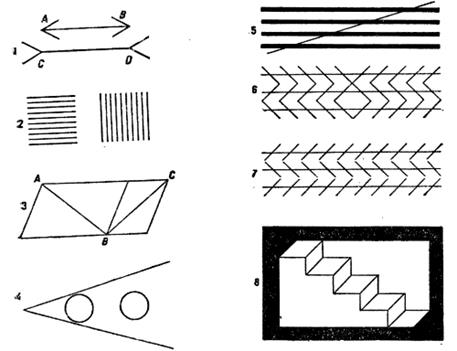
Рис. 391. Обманы зрения

Параллельные прямые, пересеченные рядом наклонных секущих, кажутся сходящимися (рис. 391, 6 и 7). Фигура, изображенная на рис. 391, 8 (лестница Шредера), может казаться или в виде ступенек лестницы, или в виде ступенчатой ниши. Ту или иную иллюзию можно вызывать по своему произволу. Ушедший вперед пешеход кажется выше заднего (рис. 392).

Рис. 392. Обман зрения

Точно так же по своему желанию можно на фигуре рисунка 393 увидать два черных профиля (силуэта) на белом фоне или белую вазу на верном фоне. Этот опыт выявляет свойство глаза выделять какой- либо один предмет в роли рассматриваемой „картины“ и все остальное относить к общему «фону».

Рис. 393. Обман зрения

Если рисунок спирали Плато (рис. 394) привести в поступательное движение по часовой стрелке, то спираль кажется вращающейся; подобную же иллюзию вращения дает фигура, придуманная С. Томсоном (рис. 395), если ее привести в круговое вращение.

Рис. 394. Иллюзия движения

Рис. 395. Иллюзия движения

Эффектный опыт рекомендует Ш. Бидвелл. Перед фонарем устанавливают ширму с узкой вертикальной щелью и вращающийся диск со спиральным вырезом (рис. 396). При вращении диска по часовой стрелке на экране светлое пятно движется снизу вверх; после наблюдения в течение примерно 30—50 сек. вращение прекращают; наблюдателям кажется, что пятно продолжает двигаться, но вниз.

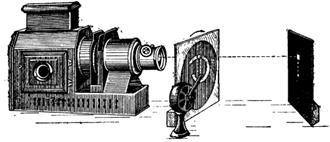
Рис. 396. Опыт Бидвелла

Продемонстрировать обманы зрения можно двояко: во-первых, можно изготовить стенные таблицы, пользуясь хотя бы рисунком 391; во-вторых, можно на основании того же рисунка сделать диапозитивы (рис. 397).

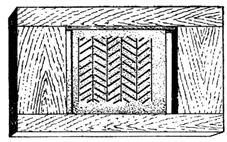
Рис. 397. Диапозитив для проектирования обманов зрения

Для этого берут стекла, покрытые слоем желатина (т. е. фотопластинка, обработанная проявителем и фиксажем), и на слое желатина копируют тушью нужный рисунок, подложив его под стекло. Можно, наконец, протравить рисунок на стекле посредством фтористого водорода. Для этого стекло покрывают тонким слоем воска, погрузив стекло в расплавленный воск. Вынув стекло, оставляют его в горизонтальном положении до застывания воска. На слое воска острием иглы или ножа процарапывают до стекла требуемый рисунок подложив его под стекло и ярко осветив снизу. По размеру стекла из листа свинца сгибают ванночку и крышку к ней (рис. 398).

Рис. 398. Свинцовая ванна

В ванночку ставят две согнутые полоски свинца (h = 1 см), чтобы на них легло стекло своими краями. Посередине ванночки насыпают небольшую кучку (половину чайной ложки) фтористого кальция. Облив его серной кислотой, тотчас же кладут стекло рисунком вниз и закрывают крышкой.

В таком положении оставляют стекло на 1—2 часа. Затем, вынув стекло, соскабливают воск и смывают его остатки бензином. Вследствие сильной ядовитости фтористого водорода травление стекла надо производить с большой осторожностью, обязательно на открытом воздухе или в вытяжном шкафу. По окончании работы ванночку надо тщательно промыть водой.

Тем или иным способом полезно изготовить три пары стекол по рисунку 399.

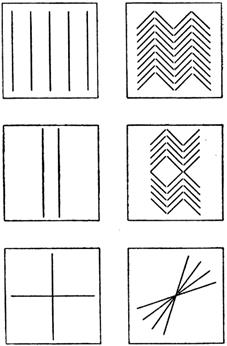
Рис. 399. Чертежи к диапозитивам обманов зрения

Каждая пара вставляется в рамку, в пазах которой стекла должны свободно перемещаться. Полученный диапозитив (рис. 397) проектируют на экран, сперва установив параллельные линии в свободных промежутках между рядами наклонных, а затем сдвигом стекла налагают параллельные линии на середину полосы, занятой секущими, и параллельные прямые покажутся сходящимися. У третьей пары прямой угол между двумя прямыми кажется тупым, как только в него будет вдвинут веер из расходящихся прямых.