Внезапное трехфазное короткое замыкание синхронного генератора

При исследовании статических режимов синхронной машины мы использовали уравнение напряжений

,

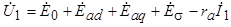полученное из физических представлений на основе понятия о вращающихся магнитных полях. Такой подход позволил сравнительно просто выявить основные свойства и характеристики синхронных машин в установившихся режимах. Поведение же синхронной машины в динамических режимах описывается системой дифференциальных уравнений. Однако для качественного анализа электромагнитных переходных процессов также удобно использовать физический подход.

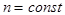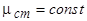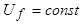Рассмотрим внезапное симметричное короткое замыкание синхронного генератора из режима холостого хода при , и . При анализе внезапного короткого замыкания основной интерес представляют величины токов обмотки статора и характер их изменения во времени.

Расчет токов короткого замыкания трехфазного явнополюсного генератора с обмоткой возбуждения f и двумя короткозамкнутыми эквивалентными демпферными обмоткам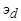и и 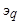по осям d и q ротора (рис. 5.56) может быть выполнен с помощью дифференциальных уравнений магнитосвязанных контуров синхронной машины:

; ;

; ;

; .

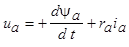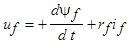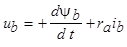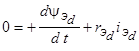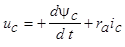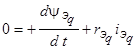Однако строгое аналитическое решение данной системы уравнений оказывается достаточно сложным. С целью упрощения воспользуемся теоремой о постоянстве потокосцепления короткозамкнутого сверхпроводящего контура. Поскольку в сверхпроводящем контуре активное сопротивление 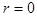, то уравнение напряжения для него имеет вид

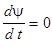
и, следовательно, потокосцепление 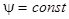. Любые изменения потока взаимоиндукции сверхпроводящего контура вызывают протекание тока в нем такой величины и такого направления, что поле этих токов компенсирует изменение потока взаимоиндукции и поэтому результирующий поток остается неизменным.

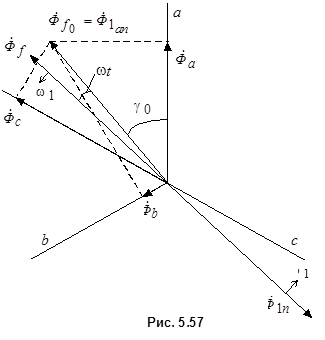
Реальные контуры синхронных машин обладают малым активным сопротивлением, и для начального периода короткого замыкания можно принять активные сопротивления всех обмоток равными нулю.

Пусть в первый момент короткого замыкания ( 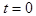) положение вектора потока обмотки возбуждения 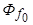определяется углом 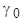относительно фазы «а» статора (рис. 5.57). Этот поток образует с обмотками статора потокосцепления

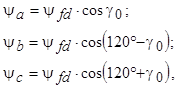
где 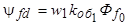- максимальное потокосцепление фазы в момент совпадения ее магнитной оси с осью d ротора.

Согласно теореме о постоянстве потокосцепления полные потокосцепления фаз 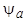, , 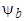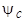должны оставаться неизменными и при 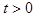. В произвольный момент времени t положение вектора 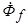задается углом 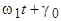, т.е. потокосцепления фаз статора с этим потоком будут меняться с течением времени. Для того, чтобы полные потокосцепления фаз статора остались неизменными, в них должны возникнуть системы апериодических 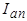и периодических 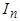токов. Система апериодических токов 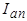создает поток реакции якоря 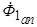, неподвижный относительно статора и равный в первый момент короткого замыкания потоку 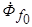, а система периодических токов 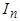создает поток реакции якоря 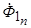, вращающийся синхронно с потоком 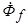, но направленный в противоположную сторону.

Возникновение двух магнитных полей реакции якоря вызывает, в соответствии с теоремой о постоянстве потокосцеплений замкнутых роторных контуров, токи, противодействующие образованию новых магнитных полей и тем самым обеспечивающие постоянство потокосцеплений соответствующих обмоток. Внезапное возникновение вращающегося магнитного поля реакции якоря 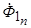, неподвижного относительно ротора, вызывает в замкнутых роторных контурах апериодические токи 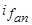, , 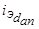, 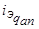а неподвижное поле реакции якоря 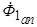наводит в короткозамкнутых роторных контурах периодические токи 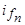, , 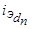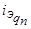частоты 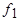, которые постепенно затухают по мере затухания апериодических токов статора.

Трансформаторная связь между апериодическими токами ротора и периодическими токами статора может быть выражена уравнениями потокосцеплений. В соответствии с теоремой о постоянстве потокосцеплений каждой обмотки по оси d имеем

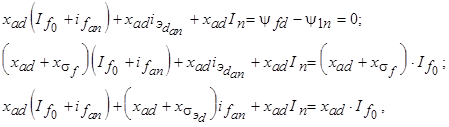
где 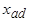- индуктивное сопротивление реакции якоря по продольной оси; 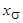, , 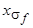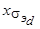- индуктивные сопротивления обмоток статора и ротора по продольной оси.

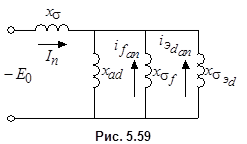
Первое уравнение определяет потокосцепление фазы «а» при . Второе уравнение определяет потокосцепление обмотки возбуждения, а третье - потокосцепление эквивалентной демпферной обмотки по оси d. Уравнения потокосцеплений могут быть преобразованы к более удобному для анализа виду, если заменить 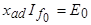и сгруппировать члены, зависящие от :

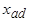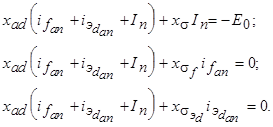
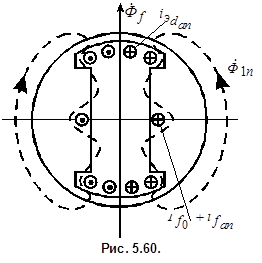
Этим уравнениям соответствует схема замещения (рис.5.59). Входное сопротивление схемы

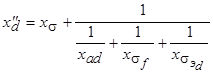
называется сверхпереходным индуктивным сопротивлением обмотки статора по оси d. Величина сопротивления 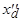зависит, главным образом, от сопротивлений рассеяния обмоток статора и ротора. Порядок этого сопротивления 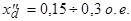Физически малая величина сопротивления 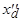объясняется следующим. В результате действия апериодических токов ротора поток реакции якоря замыкается по путям рассеяния демпферной обмотки и обмотки возбуждения (рис. 5.60). Проводимость для потока 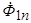снижается, и сопротивление 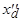оказывается небольшим.

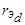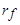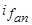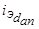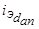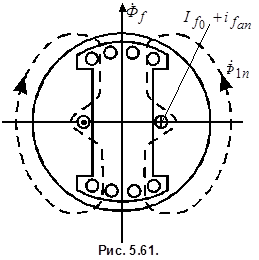
Так как сопротивления роторных обмоток и не равны нулю, то с течением времени апериодические составляющие и затухают. Токи демпферной обмотки затухают быстрее, так как сопротивление демпферной обмотки на порядок выше, чем сопротивление обмотки возбуждения. После затухания апериодического тока поток 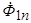частично проходит через ротор (рис. 5.61), поэтому проводимость для потока 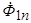возрастает. Схема замещения в этом случае (рис. 5.62) не содержит сопротивления рассеяния демпферной обмотки. Входное сопротивление схемы

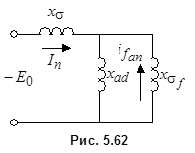
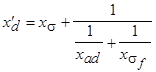
называется переходным индуктивным сопротивлением обмотки статора по оси d. В сравнении с 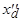сопротивление 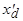имеет большую величину,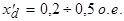

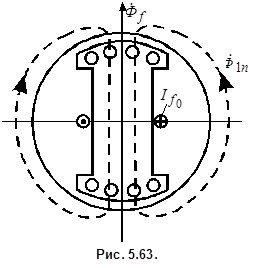
В дальнейшем по мере затухания апериодического тока 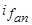в обмотке возбуждения поток реакции якоря 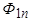все больше проникает в ротор. Когда апериодическая составляющая тока ротора полностью затухнет, поток 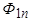будет беспрепятственно проходить через ротор (рис. 5.63). В итоге схема замещения будет содержать два последовательно соединенных сопротивления (рис. 5.64). Входное сопротивление схемы

представляет собой полное индуктивное сопротивление машины по продольной оси в установившемся режиме.

Решая первое уравнение потокосцеплений, находим периодическую составляющую тока якоря

,

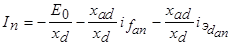или .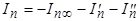

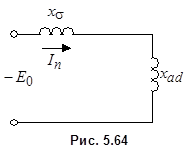
Первый член этого уравнения соответствует установившемуся току короткого замыкания, индуцируемому в обмотке якоря током возбуждения 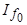, а два других члена - составляющим тока якоря, индуцируемым апериодическими токами ротора 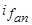и 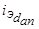. Знак «-» означает, что поле реакции якоря 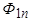носит размагничивающий характер. Согласно схеме замещения (рис. 5.59) периодический ток реакции якоря 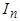в первый момент короткого замыкания определяется сопротивлением :

,

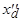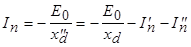а после затухания апериодического тока демпферной обмотки (рис. 5.61) ток 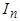определяется сопротивлением :

.

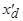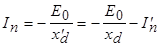Данные соотношения позволяют определить токи и :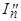

; .

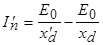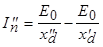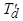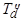Апериодические токи обмотки возбуждения и демпферной обмотки затухают с постоянными времени и соответственно. Постоянная времени 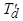определяется из схемы рис. 5.61, если учесть в контуре обмотки возбуждения сопротивление :

.

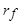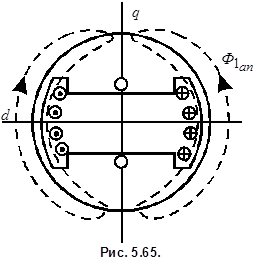
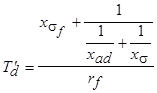Она называется постоянной времени переходного процесса. Постоянная времени сверхпереходного процесса 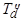определяется из схемы замещения рис.5.59, если учесть сопротивление 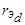в контуре демпферной обмотки:

.

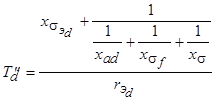Таким образом, периодическая составляющая тока якоря 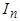с течением времени будет изменяться по закону

.

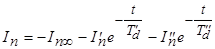Отсюда получаем мгновенное значение периодического тока короткого замыкания в фазе «а»:

.

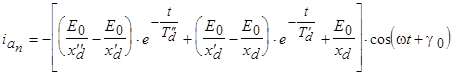Рассмотрим закон изменения апериодической составляющей тока статора 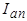. Магнитный поток 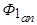, созданный этим током, неподвижен в пространстве, поэтому при вращении ротора он будет замыкаться либо по продольной, либо по поперечной оси. Реакция ротора на внезапное появление потока по продольной оси рассмотрена выше (см. рис. 5.59). Аналогичная реакция имеет место и при возникновении потока по поперечной оси (рис. 5.65).

Поэтому схема замещения синхронной машины по оси q будет иметь вид, представленный на рис. 5.66. Входное сопротивление схемы

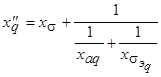
называется сверхпереходным индуктивным сопротивлением синхронной машины по поперечной оси.

В первый момент короткого замыкания при апериодическая составляющая равна и обратна по знаку периодической составляющей

.

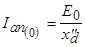Так как этот ток является свободным и не поддерживается внешними источниками, то он с течением времени затухает до нуля,

,

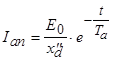где 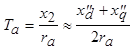- постоянная времени обмотки статора.

Реакция ротора на постоянный магнитный поток (рис. 5.59 и 5.65) аналогична реакции на поток обратной последовательности, поэтому постоянная 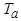определяется индуктивным сопротивлением .

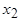При магнитной или электрической несимметрии ротора апериодическая составляющая 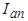будет испытывать периодические колебания между 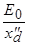и 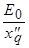с двойной частотой:

.

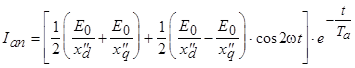Для произвольного положения ротора в первый момент короткого замыкания апериодическая составляющая тока фазы «а» статора определится из выражения

.

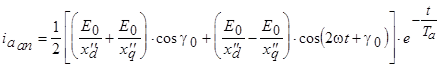Характер изменения во времени составляющих 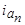, 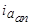и полного тока 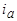фазы при трехфазном коротком замыкании для показан на рис. 5.67.

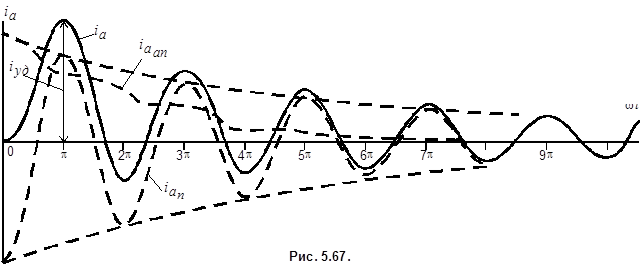
Наибольший ток короткого замыкания называется ударным током короткого замыкания 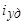. Ток 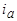достигает ударного значения примерно через полпериода после начала короткого замыкания. Величина ударного тока 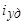с учетом затухания апериодических токов статора и ротора определяется по формуле

.

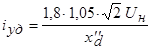Ток короткого замыкания создает весьма опасные электродинамические усилия в зоне лобовых частей обмотки статора. Эти усилия стремятся отогнуть лобовые части обмотки статора к торцевой поверхности сердечника статора. ГОСТ ограничивает величину ударного тока короткого замыкания мощных машин значением .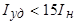

Переходные токи короткого замыкания создают также знакопеременный момент на валу машины. Амплитуда этого момента может в 5¸15 раз превышать номинальный момент, поэтому его необходимо учитывать при расчете на прочность валов и муфт, соединяющих синхронный генератор с турбиной. Тепловые воздействия токов короткого замыкания не представляют большой опасности для генератора, так как длительность короткого замыкания обычно не превышает 1 с.