Теорема отсчётов Котельникова
Аналитическое описание процесса дискретизации
Под ДИСКРЕТИЗАЦИЕЙ понимают преобразование аналогового сигнала х(t) в последовательность отсчётов его мгновенных значений, взятых через интервалы времени ∆t:
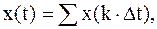
| (1.1) | |||
| где | 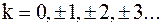
| |||
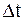
| – | шаг дискретизации; | ||
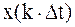
| – | отсчёты мгновенных значений. | ||
Для аналитического описания дискретизации используют решётчатую функцию 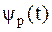 вида:
вида:
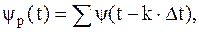
| (1.2) | |||
| где | 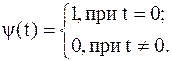
| |||
Введение функции 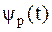 позволяет процесс дискретизации аналогового сигнала x(t) выразить произведением вида:
позволяет процесс дискретизации аналогового сигнала x(t) выразить произведением вида:
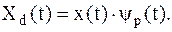
| (1.3) |
|
| Рисунок 1.1 – Дискретизация сигнала |
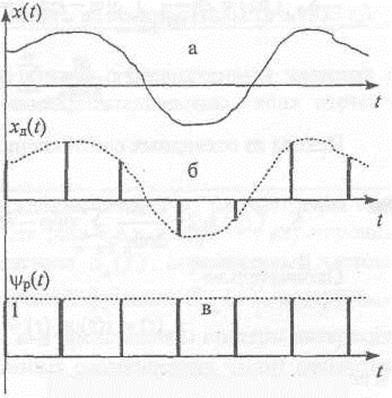
Решётчатая функция обладает фильтрующим свойством: если дельта-функция присутствует под интегралом, то результат интегрирования равен значению остального подынтегрального выражения в этой точке:
| (1.3) |
Из (1.3) вытекает, что процесс дискретизации сигналов можно реализовать на перемножителе.
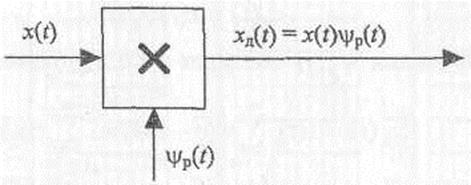
|
| Рисунок 1.2 – Структурная схема дискретизатора |
Выводы
1. Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизацией или квантованием по уровню. Квантование по уровню широко используется в цифровых автоматах.
Теорема отсчётов Котельникова
Важнейшим вопросом при дискретизации является выбор частоты дискретизации.
Ответ на этот вопрос даёт теорема отсчётов, которая часто называется теоремой Котельникова.
Теорема отсчётов.
Любой F-финитный сигнал (сигнал с ограниченным спектром  ) точно определяется последовательностью своих отсчётов, взятых через интервалы:
) точно определяется последовательностью своих отсчётов, взятых через интервалы:
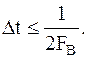
| (2.1) |
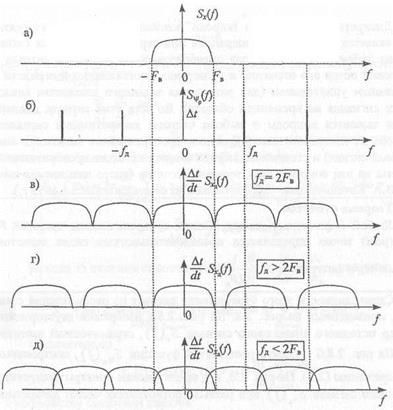
Справедливость этого утверждения следует из рассмотрения спектров, приведенных на рисунке 2.1.
|
| Рисунок 2.1 – Спектры сигналов в процессе дискретизации |
На рисунке 1а изображён двухсторонний спектр исходного аналогового сигнала 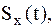 ограниченный частотой
ограниченный частотой 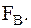
На рисунке 1б – спектр решётчатой функции.
На рис. 1, в-д представлены спектры дискретизированного сигнала при разных соотношениях 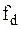 и
и 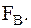 .
.
Следует обратить внимание, что в процессе дискретизации сигнала его спектр периодически повторяется по оси частот с периодом 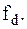
Дата добавления: 2017-11-21; просмотров: 947;











