Восстановление сигнала в аналоговой форме по его отсчётам

Исходя из свойства взаимно однозначного соответствия временного и спектрального представлений сигнала, можно утверждать, что точное восстановление сигнала в аналоговой форме по его отсчетам возможно, если из спектров 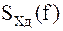(рисунок 2.1, в – д) можно получить спектр 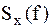(рисунок 2.1, а). Очевидно, что это достижимо:

1. Фильтрациейдискретизированного сигнала с помощью идеального ФНЧ с частотой верхнего среза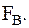

2. Только в случае 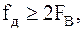когда отсутствует наложение спектров, такое, как показано на рисунке 2.1, д.

Таким образом, процедура восстановления сигнала по отсчетам может быть осуществлена идеальным ФНЧ с передаточной функцией:

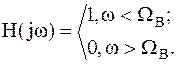
	(2.2)
где		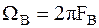–	нормированная частота среза ФНЧ;
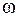
		–	амплитуда.

и, соответственно, с импульсной характеристикой

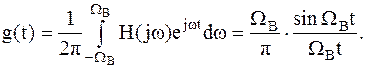
(2.3)

Поскольку импульсная характеристика цепи есть ее реакция на воздействие в виде 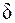– функции 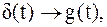то легко определить реакцию идеального ФНЧ на дискретизированный сигнал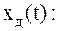

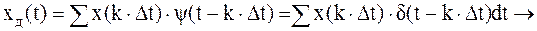
	(2.4)

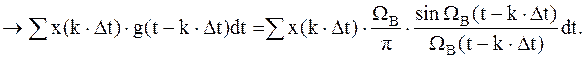
Выражение (2.5) известно в литературе как ряд Котельникова (с масштабным коэффициентом с) и представляет собой частный случай обобщенного ряда Фурье, где базисом является система функций 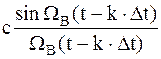, а коэффициентами разложения служат отсчеты мгновенных значений сигнала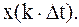

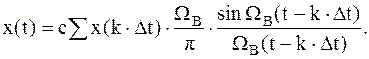
(2.5)

На практике абсолютно точное восстановление сигналов по их от­счетам невозможно по следующим причинам:

1. Идеальный ФНЧ – физически нереализуемая цепь, так как его импульсная характеристика отлична от 0 при t < 0. Характеристики реальных ФНЧ могут быть приближены к идеальным лишь с определенной погрешностью, тем меньшей, чем больше задержка.

2. Реальные сигналы являются Т-финитными, а следовательно, имеют неограниченный по частоте спектр. Если все же спектр сигнала ограничить частотой F_B, то на интервале существования сигнала T число независимых отсчетов N, определяющих сигнал с заданной погрешностью, становится конечным.

При осуществлении дискретизации сигнала, когда частота дискре­тизации 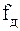выбрана, необходимо использовать антиэлайсинговый ФНЧ с частотой верхнего среза 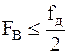для ограничения спектра сигнала и предотвращения тем самым искажений, вызванных перекрытием спектров (рисунок 2.1, д) (антиэлайсинговый – от слова «элайсинг», означающего наложение спектров).

Вывод:

1. Дискретизация сигналов широко используется в современных системах связи. Она является необходимой операцией при передаче аналоговых сигналов по цифровым каналам.

2. При выборе частоты дискретизации, способе восстановления аналоговых сигналов теоретической базой является теорема отсчётов Котельникова.

Выводы

1. Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизацией или квантованием по уровню. Квантование по уровню широко используется в цифровых автоматах.

2. Дискретизация сигналов широко используется в современных системах связи. Она является необходимой операцией при передаче аналоговых сигналов по цифровым каналам.

3. При выборе частоты дискретизации, способе восстановления аналоговых сигналов теоретической базой является теорема отсчётов Котельникова.

Заключение

Дискретизация сигналов широко используется в системах связи. Она является необходимой операцией при передаче аналоговых сигналов по цифровым каналам (для преобразования аналогового сигнала в цифровой поток его отсчетов) и в системах многоканальной передачи с временным уплотнением (для разделения заданного множества аналоговых сигналов во временной области). Во всех этих случаях важнейшими являются вопросы о выборе частоты дискретизации сигналов, способе их восстановления (обратного преобразования отсчетов в аналоговый сигнал) и степени искажений в процессе таких преобразований. Ответы на эти вопросы дает теорема отсчетов (часто называемая име­нем В.А. Котельникова – автора одного из ее доказательств в 1933 г.).

Литература

Основная:

1. Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.

Дополнительная:

1. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.

2. Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.

3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.

4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.