Доказательство теоремы отсчетов
Непрерывный входной сигнал может быть преобразован в последовательность дискретных значений, если с помощью элемента выборки-хранения через равные интервалы в моменты времени ti = Т0×i брать значения входного сигнала. Здесь f0 = 1/T0 – частота выборки. Из рис. 1.13, а, видно, что соответствующая ступенчатая функция тем ближе к непрерывной входной функции, чем меньше период выборки. Следовательно, увеличивая частоту выборки, можно обеспечить требуемую точность воспроизведения. Однако часто реализовать высокую частоту выборки оказывается затруднительно.
И 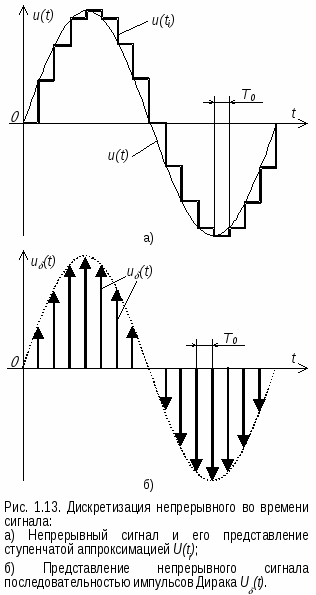 з теоремы отсчетов следует, что можно преобразовать входную функцию с помощью выборок, которые производятся на относительно низкой частоте, а затем получить сигнал, близкий к первоначальному, используя соответствующие фильтры. Для этого нужно сделать допущение, что входная функция u(t) имеет ограниченную полосу, т.е. ее спектр U(jf) для частот свыше fmмало отличается от нуля. Это условие для входного сигнала можно выполнить, пропустив предварительно сигнал через фильтр нижних частот. При этом сигнал не будет заметно искажаться.
з теоремы отсчетов следует, что можно преобразовать входную функцию с помощью выборок, которые производятся на относительно низкой частоте, а затем получить сигнал, близкий к первоначальному, используя соответствующие фильтры. Для этого нужно сделать допущение, что входная функция u(t) имеет ограниченную полосу, т.е. ее спектр U(jf) для частот свыше fmмало отличается от нуля. Это условие для входного сигнала можно выполнить, пропустив предварительно сигнал через фильтр нижних частот. При этом сигнал не будет заметно искажаться.
Ступенчатую функцию, показанную на рис. 1.13, а, трудно представить в аналитической форме. Как показано на рис. 1.13, б, ее можно заменить последовательностью импульсов Дирака с той же вольтсекундной площадью:
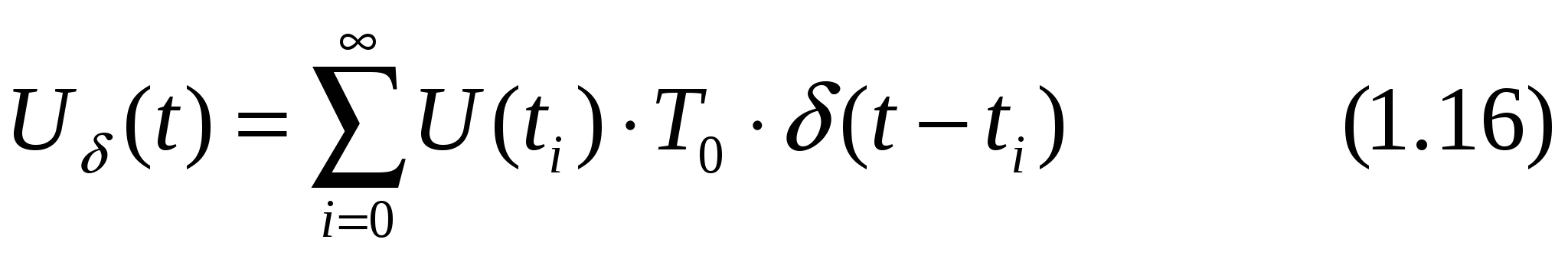
В 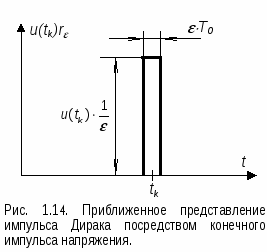 еличина U(ti)T0 изображается стрелкой; она является характеристикой импульса, поскольку по определению импульсы Дирака имеют бесконечно большую амплитуду и бесконечно малую длительность. Площадь каждого из этих импульсов имеет, однако, конечное значение; именно она и характеризует импульс. На рис. 1.14 импульс Дирака в первом приближении представлен прямоугольным импульсом re. При этом справедлив предельный переход:
еличина U(ti)T0 изображается стрелкой; она является характеристикой импульса, поскольку по определению импульсы Дирака имеют бесконечно большую амплитуду и бесконечно малую длительность. Площадь каждого из этих импульсов имеет, однако, конечное значение; именно она и характеризует импульс. На рис. 1.14 импульс Дирака в первом приближении представлен прямоугольным импульсом re. При этом справедлив предельный переход:
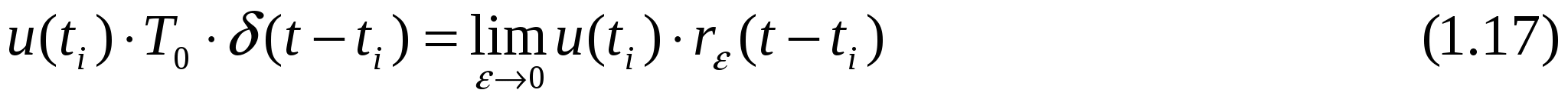
Для доказательства теоремы отсчетов рассмотрим функцию u(t) с преобразованием Фурье U(jw) (или U(jf)). Причем U(jf)=0 при |f|>fm, т.е. спектр сигнала ограничен по частоте. Рассмотрим также дополнительную функцию – периодический спектр Uп(jf) с периодом f0, совпадающий с исходным спектром U(jf) на интервале частот -f0/2< f < +f0/2 (см. рис. 1.15).
Периодическая функция частоты f Uп(jf) с периодом f0 может быть представлена в виде ряда Фурье в комплексной форме:
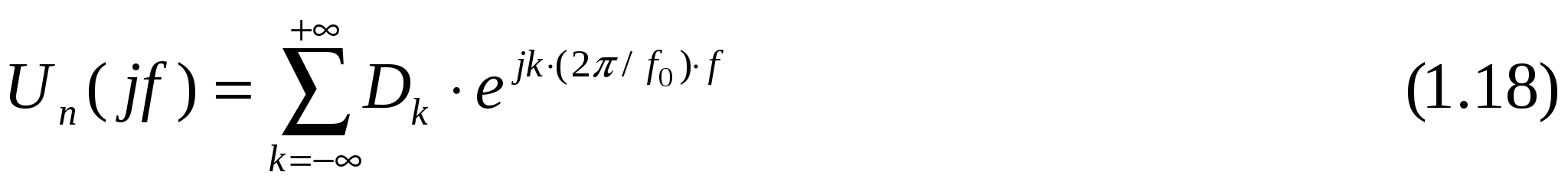
с коэффициентами:
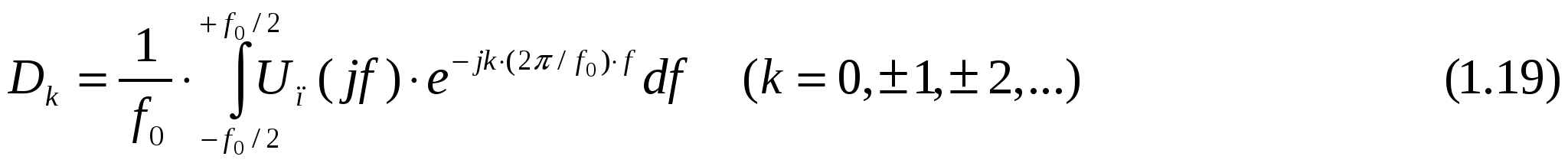
Представим выражение для дискретизируемого сигнала во временной области u(t) через его частотный спектр U(jf) c помощью обратного преобразования Фурье (напомним, что U(jf)=0 при |f|>fm, т.е. максимальная частота в спектре дискретизируемого сигнала fm):
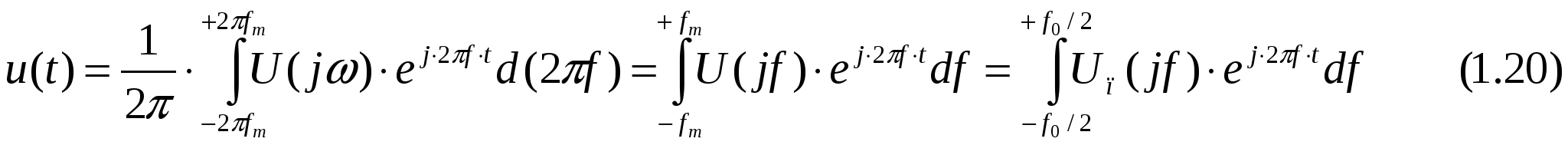
Полагая t=kT0, получаем выражение для определения выборок функции u(t), разделенных интервалами длиной T0:
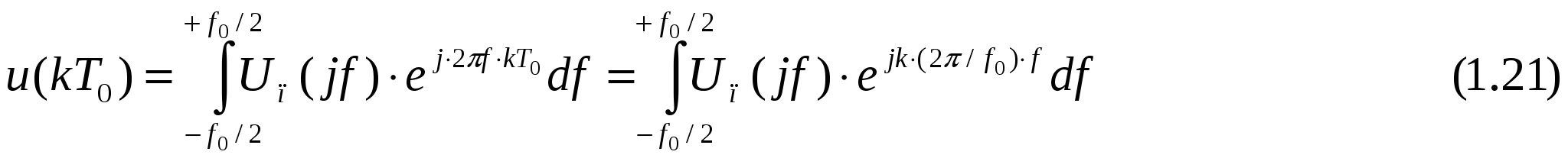
Сравнивая выражения (1.19) и (1.21), получаем коэффициенты периодически продолженного спектра:

Следовательно, если мы знаем значения сигнала u(t) в равноотстоящие моменты времени kT0 для k=0…+¥, то ряд Фурье периодически продолженного спектра Uп(jf) однозначно определяется этими выборками. Как следует из (1.22) для реальных электрических сигналов Dk=0 для k>0. В соответствии с этим выражения (1.18) и (1.19) преобразуются к нижеприведенному уточненному виду при


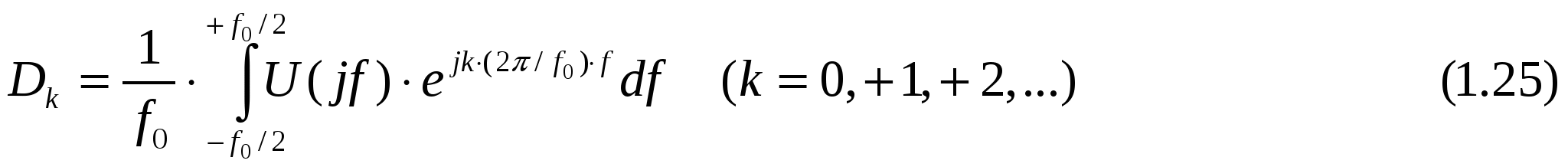
Покажем также, что при выборе частоты отсчетов f0 ³ 2fm, можно найти выражение для восстановления непрерывного аналогового сигнала по его выборкам. На интервале частот (-f0/2, f0/2) сигнал u(t) через спектр выражается в виде:
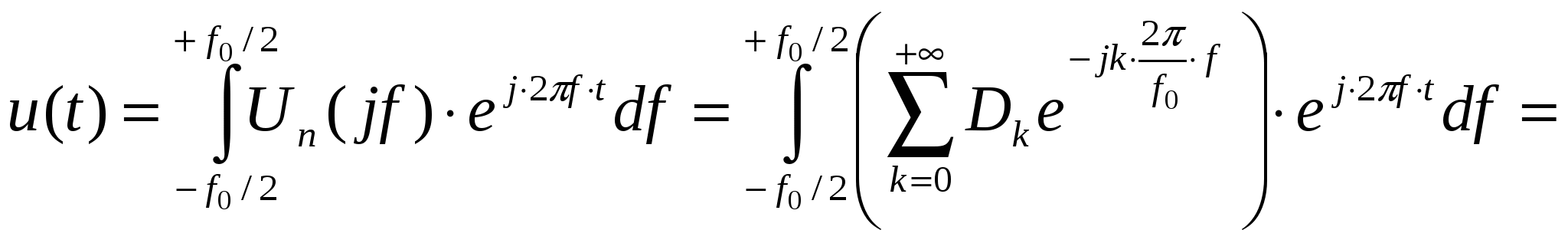
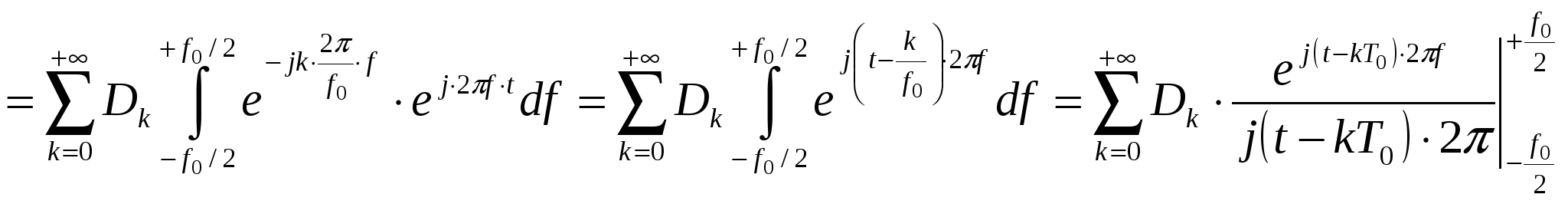
Дата добавления: 2016-12-27; просмотров: 1457;











