Теорема о внешней устойчивости резонанса в динамической системе с двумя быстрыми фазами.

Вопросы исследования устойчивости резонансов при действии возмущений рассматриваются в широком круге работ. Как правило, в работах под устойчивостью резонансов понималась устойчивость решений системы внутри асимптотически малой резонансной зоны. В то же время резонансы могут определять эволюцию медленных переменных уже на нерезонансных участках движения. Подобные явления, известные как вторичные резонансные эффекты, наблюдаются при усреднении систем с медленной эволюцией на нерезонансных участках движения. При этом, как это было показано выше, в усредненных уравнениях резонансные знаменатели входят в члены, начиная со второго приближения метода усреднения, поэтому влияние вторичных резонансных эффектов на изменение переменных является существенным при отсутствии эволюции в первом приближении. Усредняя медленно изменяющиеся переменные системы можно получить условия внешней устойчивости резонанса в нерезонансном случае. Тогда под внутренней устойчивостью следует понимать устойчивость решений в резонансной области. Прежде чем получить условия внешней устойчивости резонансов при движении твердого тела требуется дать строгое определение внешней устойчивости резонансов применительно к системе стандартного вида с медленно изменяющимися параметрами.

Рассматриваемая система является двухчастотной системой с периодическими возмущениями

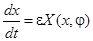, (3.1)

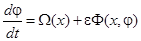, (3.2)

где 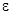- малый параметр, 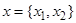- вектор медленных переменных, 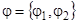- быстрые фазы; 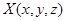, 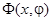- возмущения, периодические по фазам 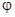c периодом равным 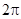и раскладывающиеся по 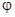в ряд Фурье без нулевого члена; 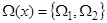- частоты системы (3.1)-(3.2). Резонансное соотношение частот в системе (3.1)-(3.2) имеет вид: 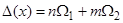, где n и m - некоторые постоянные.

Резонансные зоны, традиционно имеющие порядок 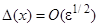, делят фазовую плоскость 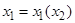на нерезонансные области. Причем резонансное соотношение 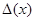, как и коэффициенты разложения функций X, 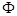в ряд Фурье, не меняют свои знаки при движении на каждом из нерезонансных участков.

Внешнюю устойчивость резонанса 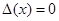в системе (3.1)-(3.2) можно определить следующим образом.

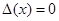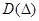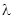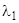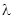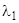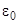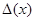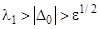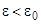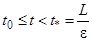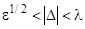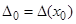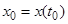Определение. Резонанс внешне устойчив в некоторой нерезонансной области , если для любого >0, можно найти такие ( > >0), >0, L>0, что для всех , определенных из системы (3.1)-(3.2), при и 0< на интервале выполняется условие , где , , а 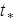-определяет момент выхода 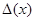на границу 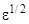- окрестности резонанса.

Следовательно, о внешней устойчивости резонанса 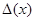=0 в случае нескольких медленных переменных можно говорить лишь применительно к некоторой области .

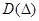Сформулируем теорему о внешней устойчивости резонанса 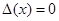в системе (3.1)-(3.2). При получении этой теоремы используются схемы доказательств, приведенные в работах Хапаева М.М.

Условия теоремы о внешней устойчивости резонанса 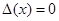для системы (3.1)-(3.2) имеют следующий вид:

1) существует положительно определенная по переменной 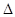функция Ляпунова 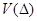системы (3.1)-(3.2), допускающая по переменной 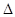бесконечно малый высший предел, которая является ограниченной в области 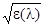< < 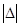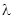и имеет вид ;

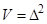2) равномерно относительно 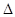из области 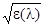< < 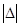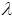существует среднее

,

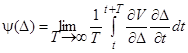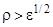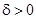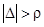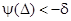и для всякого можно указать такое , что если , то (при );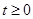

3) существуют суммируемые функци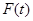и и 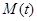, постоянные 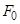и 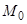, а также неубывающая функция 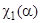, , 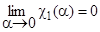такие, что в области 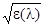< < 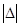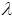имеют место неравенства:

, ,

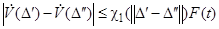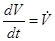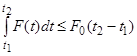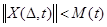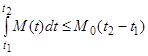, , на любом конечном отрезке .

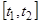Условия позволяют сформулировать следующую теорему [19].

Теорема. При выполнении условий 1) - 3) резонанс 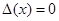внешне устойчив.

Доказательство теоремы содержится в статье Любимова В.В. в журнале «Известия РАН. Механика твёрдого тела».

Таким образом, метод исследования внешней устойчивости резонанса можно сформулировать в виде следующего алгоритма:

1. Динамическая система приводится к стандартной форме систем с быстрыми и медленными переменными, для последующего ее усреднения в нерезонансном случае.

2. Динамическая система усредняется в нерезонансном случае с получением двух (трех при равенстве нулю первых двух и т.д.) первых приближений метода усреднения.

3. Вводится функция Ляпунова в форме квадрата резонансной расстройки частот.

4. Определяется усредненное выражение для производной функции Ляпунова с учетом высших приближений.

5. Производится анализ знака усредненного выражения для производной функции Ляпунова с учетом высших приближений.

Замечание. Положительный знак усредненного выражения для производной функции Ляпунова свидетельствует о внешней неустойчивости резонанса, а его отрицательный знак – о внешней устойчивости рассматриваемого резонанса.