Практическое занятие 2. Анализ внешней устойчивости резонансов при движении космических аппаратов в атмосфере.
Квазилинейная динамическая система.
Проблема устойчивости резонансов при возмущенном движении относительно центра масс возвращаемых космических аппаратов в атмосфере рассматривалась в значительном количестве публикаций и в других работах. При этом устойчивость резонансов исследовалась в асимптотически малой окрестности данных резонансов. В работах применительно к системам общего вида с быстрыми и медленными переменными было введено понятие «внешней устойчивости резонанса». Внешняя устойчивость резонанса сопровождается эволюцией медленных переменных на нерезонансных участках движения, прилегающих к рассматриваемому резонансу. При этом, внешне устойчивый резонанс множеством, «притягивающим» траектории. Напротив, внешне неустойчивый резонанс представляет собой множеством, «отталкивающим» траектории. В дальнейшем, были сформулировано определение и получены условия внешней устойчивости резонанса в нелинейной системе с медленными и быстрыми переменными. Явление внешней устойчивости резонансов было обнаружено в задаче о возмущенном орбитальном движении твердого тела с сильным магнитом в геомагнитном поле. Применительно к задаче о спуске в атмосфере космического аппарата с малой асимметрией явление внешней устойчивости резонансов было изучено в следующих работах. В указанных исследованиях внешней устойчивости резонансов не учитывалась эволюция характеристик движения центра масс. Кроме того, величины смещений центра масс и аэродинамическая асимметрия формы предполагались неизменными, что несколько уменьшает практическую значимость полученных в указанных работах результатов.
ПОСТАНОВКА ЗАДАЧИ. Ставиться задача по исследованию внешней устойчивости главного резонанса при спуске в атмосфере асимметричного космического аппарата при малых углах атаки. Космический аппарат (КА) рассматривается как твердое тело массой 75 кг и имеет форму, близкую к конической. На аппарат действует аэродинамические моменты: восстанавливающий и возмущающий. Восстанавливающий момент пропорционален относительно немалому расстоянию между центром масс и центром приложения аэродинамических сил. В качестве возмущений на КА действуют механические моменты от малой аэродинамической и массовой асимметрий. При исследовании внешней устойчивости требуется рассмотреть только главный резонанс. Известно [12], что нерезонансная эволюция угловой скорости при простейшем главном резонансе превышает соответствующие значения эволюции при учете резонансов высших порядков. Предполагается произвести анализ внешней устойчивости главного резонанса в квазилинейном случае (при малых значениях угла атаки). Квазилинейная постановка задачи позволит произвести подробный приближенно-аналитический анализ условия внешней устойчивости и определить возможные случаи устойчивости и неустойчивости главного резонанса, которые подтверждаются численными результатами. Кроме того, для стабилизации вращательного движения КА вводится аналитическая зависимость, позволяющая уменьшить величину аэродинамической асимметрии при атмосферном спуске КА. Приводятся численные результаты, отражающие явление внешней устойчивости при неизменных и изменяющихся параметрах асимметрии.
Рассмотрим движение спускаемого КА с малыми значениями угла атаки в случае положительных 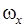 при выполнении условия
при выполнении условия 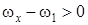 . Случай положительных значений
. Случай положительных значений 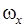 при
при 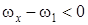 может быть рассмотрен по аналогии, как и случаи отрицательных
может быть рассмотрен по аналогии, как и случаи отрицательных 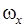 .
.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ. Взаимное положение связанной с аппаратом системы координат OXYZ и орбитальной системы координат 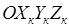 определяется посредством трех углов ориентации: пространственного угла атаки
определяется посредством трех углов ориентации: пространственного угла атаки 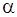 п, аэродинамического угла крена
п, аэродинамического угла крена 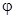 п и скоростного угла крена γa. В дальнейшем нижние индексы в данных углах ориентации не указываются.
п и скоростного угла крена γa. В дальнейшем нижние индексы в данных углах ориентации не указываются.
Приближенная квазилинейная система уравнений движения КА с малой асимметрией относительно центра масс в атмосфере, полученная в статье [13], имеет вид:
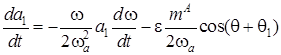 , (1)
, (1)
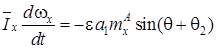 , (2)
, (2)
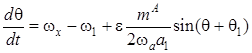 , (3)
, (3)
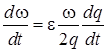 , (4)
, (4)
где ε - малый параметр, характеризующий малость параметров массовой и аэродинамической асимметрии, а также медленность изменения ω; a1 – амплитуда угла атаки, являющаяся углом между ось OX и вектором кинетического момента КА; 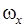 - угловая скорость КА относительно оси OX;
- угловая скорость КА относительно оси OX; 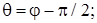
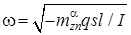 ;
; 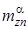 - частная производная коэффициента восстанавливающего аэродинамического момента
- частная производная коэффициента восстанавливающего аэродинамического момента 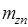 по углу атаки a при a=0;
по углу атаки a при a=0; 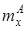 ,
, 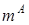 ,
, 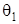 ,
, 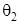 - функции, характеризующие величину и взаимное расположение массовой и аэродинамической асимметрий;
- функции, характеризующие величину и взаимное расположение массовой и аэродинамической асимметрий;
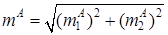 ,
, 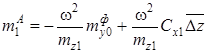 ,
,
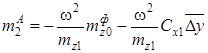 ;
; 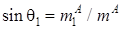 ;
; 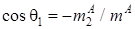 ;
;
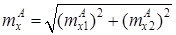 ,
, 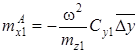 ,
,
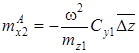 ;
; 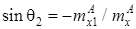 ;
; 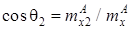 ;
; 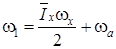 ;
; 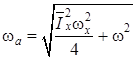 ;
;
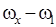 - резонансное соотношение частот; q - скоростной напор; S и L - площадь миделевого сечения и длина аппарата;
- резонансное соотношение частот; q - скоростной напор; S и L - площадь миделевого сечения и длина аппарата; 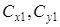 - коэффициенты аэродинамических сил [13];
- коэффициенты аэродинамических сил [13]; 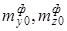 - коэффициенты малых аэродинамических моментов от асимметрии формы КА;
- коэффициенты малых аэродинамических моментов от асимметрии формы КА; 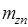 - коэффициент восстанавливающего аэродинамического момента;
- коэффициент восстанавливающего аэродинамического момента; 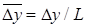 ,
, 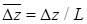 ; Dy, Dz - малые смещения центра масс КА в системе координат OXYZ;
; Dy, Dz - малые смещения центра масс КА в системе координат OXYZ; 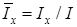 ;
; 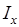 и
и 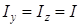 - моменты инерции аппарата относительно осей системы координат OXYZ.
- моменты инерции аппарата относительно осей системы координат OXYZ.
Приближенные квазилинейные уравнения (1)-(4) получены из системы исходных нелинейных уравнений движения КА с малой асимметрией относительно центра масс методом асимптотического расщепления решений с учетом предположения о малости значений пространственного угла атаки [13], [3]. Предположим, что угол между вектором воздушной скорости и вектором кинетического момента равен нулю (a2 =0). В этом случае получаем, что угол атаки равен первой амплитуде: α=a1.
Квазилинейные уравнения (1)-(4) учитывают возможность реализации главного резонанса, наблюдающегося при выполнении равенства:
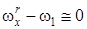 . (5)
. (5)
Из решения этого уравнения можно определить резонансное значение угловой скорости 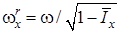 .
.
Квазилинейная система уравнений (1)-(4) рассматривается совместно с уравнениями, описывающими движение центра масс КА. Для КА, близкого по форме к осесимметричной, данные уравнения имеют вид [1]:
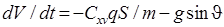 , (6)
, (6)
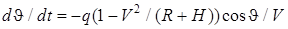 , (7)
, (7)
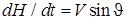 . (8)
. (8)
Здесь 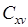 - известный аэродинамический коэффициент,
- известный аэродинамический коэффициент, 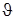 - местный угол наклона траектории, m - масса аппарата, V - воздушная скорость КА, R - радиус Марса, H - высота полёта КА.
- местный угол наклона траектории, m - масса аппарата, V - воздушная скорость КА, R - радиус Марса, H - высота полёта КА.
Уравнение (1)-(3) содержат в правых своих частях быструю фазу θ, что существенно затрудняет применение данных уравнений для анализа эволюций угловой скорости 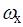 . С целью упрощения уравнения (2) произведем усреднение данного уравнения по быстрой фазе θ на нерезонансных участках движения. Усреднения уравнение (2) с учетом двух первых приближений известным методом [14],[15], получаем:
. С целью упрощения уравнения (2) произведем усреднение данного уравнения по быстрой фазе θ на нерезонансных участках движения. Усреднения уравнение (2) с учетом двух первых приближений известным методом [14],[15], получаем:
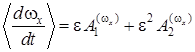 . (9)
. (9)
Здесь первое и второе приближения метода усреднения, соответственно, равны:
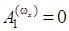 , (10)
, (10)
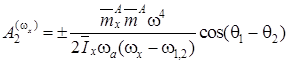 . (11)
. (11)
Безразмерные параметры асимметрии равны: 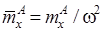 ,
, 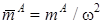 .
.
Следовательно, нерезонансную эволюцию угловой скорости 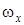 в окрестности главного резонанса определяет второе приближение (11), содержащее в знаменателе резонансное соотношение частот
в окрестности главного резонанса определяет второе приближение (11), содержащее в знаменателе резонансное соотношение частот 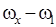 . Эволюционные явления, вызванные влиянием соотношения частот
. Эволюционные явления, вызванные влиянием соотношения частот 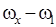 на нерезонансное изменение угловой скорости
на нерезонансное изменение угловой скорости 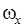 , относятся к вторичным резонансным эффектам. Применительно к задаче о спуске КА с малой массовой и аэродинамической асимметрией в атмосфере вторичные резонансные эффекты рассматривались в ряде печатных работ.
, относятся к вторичным резонансным эффектам. Применительно к задаче о спуске КА с малой массовой и аэродинамической асимметрией в атмосфере вторичные резонансные эффекты рассматривались в ряде печатных работ.
АНАЛИЗ УСЛОВИЙ ВНЕШНЕЙ УСТОЙЧИВОСТИ РЕЗОНАНСА. Для исследования внешней устойчивости главного резонанса 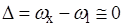 требуется рассмотреть изменение функции Ляпунова следующего вида
требуется рассмотреть изменение функции Ляпунова следующего вида 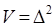 на нерезонансных участках движения. При анализе внешней устойчивости применяется выражение для усредненной производной функции Ляпунова:
на нерезонансных участках движения. При анализе внешней устойчивости применяется выражение для усредненной производной функции Ляпунова:
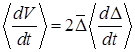 . (12)
. (12)
Далее верхние индексы для соотношения частот 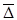 не указываются.
не указываются.
В квазилинейном случае усредненная производная 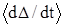 вычисляется так
вычисляется так
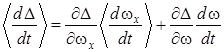 . (13)
. (13)
Здесь 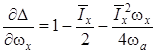 ,
, 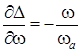 . Производные
. Производные 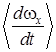 и
и 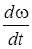 рассчитываются из выражений (9) и (4), соответственно.
рассчитываются из выражений (9) и (4), соответственно.
Согласно теореме [7] при выполнении условия (14) резонанс 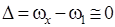 является внешне устойчивым. Условие (14) имеет вид:
является внешне устойчивым. Условие (14) имеет вид:
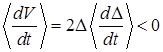 . (14)
. (14)
При выполнении условия (14) величина 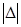 эволюционирует к резонансной области
эволюционирует к резонансной области 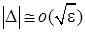 . Напротив, выполнение условия (15) обеспечивает «уход» величины
. Напротив, выполнение условия (15) обеспечивает «уход» величины 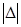 от резонансной области
от резонансной области 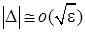 . Условие (15) записывается так:
. Условие (15) записывается так:
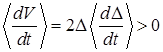 . (15)
. (15)
При выполнении условия (15) следует говорить о внешне неустойчивом резонансе 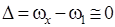 .
.
Произведем анализ условия внешней устойчивости (14) и условия внешней неустойчивости главного резонанса (15) при движении спускаемого КА с малыми значениями угла атаки в случае положительных 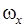 при выполнении неравенства
при выполнении неравенства 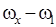 >0. Область реализации условий (14), (15) следует оценивать следующим образом:
>0. Область реализации условий (14), (15) следует оценивать следующим образом: 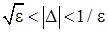 . Нижняя граница указанной области по величине
. Нижняя граница указанной области по величине 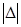 соответствует границе резонансной зоны, которая имеет порядок
соответствует границе резонансной зоны, которая имеет порядок 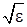 . На верхней границе данной области по величине
. На верхней границе данной области по величине 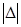 порядок малости производной
порядок малости производной 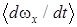 увеличивается на один порядок
увеличивается на один порядок 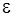 , что в соответствии с уравнением (9) приводит к стабилизации усредненных величин
, что в соответствии с уравнением (9) приводит к стабилизации усредненных величин 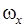 . При выполнении условия
. При выполнении условия 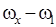 >0 усредненное значение угловой скорости содержится в области
>0 усредненное значение угловой скорости содержится в области 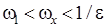 . Предположим, что соотношение моментов инерции
. Предположим, что соотношение моментов инерции 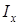 ,
, 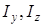 способствует выполнению условия
способствует выполнению условия 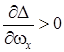 . При этом, условие (14) позволяет выделить два характерных случая реализации внешней устойчивости главного резонанса, имеющих место при одновременном выполнении условий
. При этом, условие (14) позволяет выделить два характерных случая реализации внешней устойчивости главного резонанса, имеющих место при одновременном выполнении условий 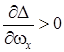 ,
, 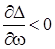 .
.
Случай 1. Из условия (14) следует, что внешняя устойчивость главного резонанса 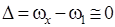 наблюдается при одновременном выполнении условий
наблюдается при одновременном выполнении условий 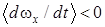 ,
, 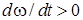 . Рис.1а на примере результатов численного интегрирования системы (1)-(8) показана реализация случая 1. Действительно, при нерезонансном уменьшении положительного значения угловой скорости
. Рис.1а на примере результатов численного интегрирования системы (1)-(8) показана реализация случая 1. Действительно, при нерезонансном уменьшении положительного значения угловой скорости 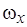 на участке увеличения величины
на участке увеличения величины 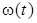 осуществляется приближение значения угловой скорости к резонансным значениям
осуществляется приближение значения угловой скорости к резонансным значениям 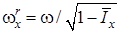 . Такое поведение системы (1)-(8) соответствует внешней устойчивости резонанса
. Такое поведение системы (1)-(8) соответствует внешней устойчивости резонанса 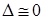 .
.
Численное интегрирование при получении результатов, показанных на рис.1, производилось при следующих исходных данных и параметрах КА: m=70 кг; S=0.2 м2, L=0.5 м, 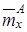 =0.04,
=0.04, 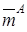 =0.08,
=0.08, 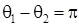 ,
, 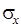 -баллистический коэффициент,
-баллистический коэффициент, 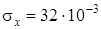 м2/кг, V(0)-начальное значение скорости КА, V(0)=3400 м/с,
м2/кг, V(0)-начальное значение скорости КА, V(0)=3400 м/с, 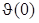 -начальное значение угла наклона траектории,
-начальное значение угла наклона траектории, 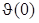 =-1 град, H(0)-начальное значение высоты полета КА, H(0)=100 км,
=-1 град, H(0)-начальное значение высоты полета КА, H(0)=100 км, 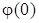 =π/6 рад,
=π/6 рад, 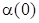 =π/50 рад,
=π/50 рад, 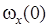 =6.7с-1 (рис.1a);
=6.7с-1 (рис.1a); 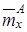 =0.03,
=0.03, 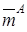 =0.1 (рис.1b).
=0.1 (рис.1b).
Случай 2. Анализ условия (14) предполагает, что реализация внешней устойчивости главного резонанса возможна также при одновременном выполнении условий 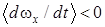 ,
, 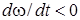 . В данном случае для реализации условия (14) требуется выполнение неравенства:
. В данном случае для реализации условия (14) требуется выполнение неравенства:
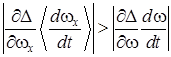 . (16)
. (16)
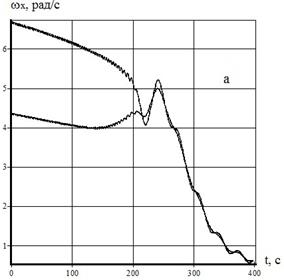
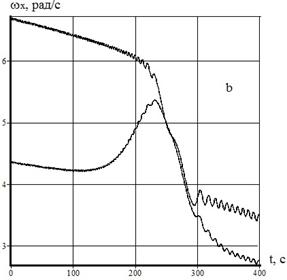
Рис.1 – Эволюция угловой скорости при внешней устойчивости резонанса
На рис.1b показано, что при нерезонансном уменьшении положительного значения угловой скорости 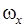 на участке уменьшения величины
на участке уменьшения величины 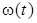 (также как на участке увеличения величины
(также как на участке увеличения величины 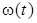 ) осуществляется приближение значения угловой скорости к резонансным значениям
) осуществляется приближение значения угловой скорости к резонансным значениям 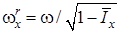 . Следовательно, поведение системы (1)-(8) в этом случае также соответствует внешней устойчивости резонанса
. Следовательно, поведение системы (1)-(8) в этом случае также соответствует внешней устойчивости резонанса 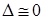 .
.
Аналогичный образом, осуществляя анализ условия (15), выделим два характерных случая (случай 3 и случай 4) реализации внешней неустойчивости главного резонанса. Пусть также имеет место одновременное выполнение условий 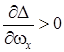 ,
, 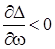 .
.
Случай 3. Условие внешней неустойчивости главного резонанса (15) выполняется при одновременном выполнении условий 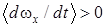 ,
, 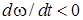 . Результаты численного интегрирования системы (1)-(8) показанные на рис.2a и рис.2b описывают реализацию случая 3. В частности, при нерезонансном увеличении положительного значения угловой скорости
. Результаты численного интегрирования системы (1)-(8) показанные на рис.2a и рис.2b описывают реализацию случая 3. В частности, при нерезонансном увеличении положительного значения угловой скорости 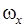 на участке уменьшения величины
на участке уменьшения величины 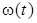 происходит удаление значений угловой скорости относительно резонансных значений
происходит удаление значений угловой скорости относительно резонансных значений 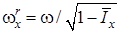 . Таким образом, поведение системы (1)-(8) в данном случае соответствует внешней неустойчивости резонанса
. Таким образом, поведение системы (1)-(8) в данном случае соответствует внешней неустойчивости резонанса 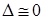 .
.
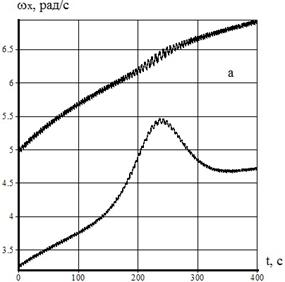
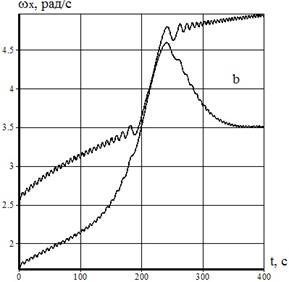
Рис.2 – Эволюция угловой скорости при внешней неустойчивости резонанса
Параметры асимметрии КА и начальное значение угловой скорости, выбранные для построения рис.2, равны следующим величинам: 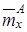 =0.05,
=0.05, 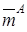 =0.1,
=0.1, 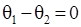 ,
, 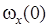 =5 с-1 (рис.2a);
=5 с-1 (рис.2a); 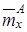 =0.02,
=0.02, 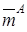 =0.08,
=0.08, 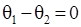 ,
, 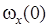 =2.6 с-1 (рис.2b). Все другие параметры КА и начальные условия движения аналогичны величинам, применяемым для построения рис.1.
=2.6 с-1 (рис.2b). Все другие параметры КА и начальные условия движения аналогичны величинам, применяемым для построения рис.1.
Случай 4. Условие внешней неустойчивости главного резонанса (15) может быть выполнено при одновременном выполнении условий 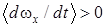 ,
, 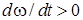 . В частности, для реализации внешней неустойчивости главного резонанса требуется выполнение условия (16). Таким образом, поведение системы (1)-(8) в данном случае также соответствует внешней неустойчивости резонанса
. В частности, для реализации внешней неустойчивости главного резонанса требуется выполнение условия (16). Таким образом, поведение системы (1)-(8) в данном случае также соответствует внешней неустойчивости резонанса 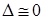 . На рис. 1b после участка, на котором происходит реализация резонанса, наблюдается удаление
. На рис. 1b после участка, на котором происходит реализация резонанса, наблюдается удаление 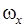 от резонансных значений
от резонансных значений 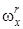 . Данный численный результат также можно характеризовать как реализацию внешней неустойчивости главного резонанса.
. Данный численный результат также можно характеризовать как реализацию внешней неустойчивости главного резонанса.
Нелинейная низкочастотная динамическая система
Первый частный случай. Рассмотрим выполнение условия внешней устойчивости главного резонанса 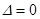 при движении КА в атмосфере при
при движении КА в атмосфере при 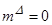 в нелинейном случае больших углов атаки. В качестве уравнений движения аппарата используется низкочастотная система уравнений (2.3)-(2.6), описывающих движение по некоторому интегральному многообразию. Данная система уравнений описывает движение КА в атмосфере в случае, близком к регулярной прецессии.
в нелинейном случае больших углов атаки. В качестве уравнений движения аппарата используется низкочастотная система уравнений (2.3)-(2.6), описывающих движение по некоторому интегральному многообразию. Данная система уравнений описывает движение КА в атмосфере в случае, близком к регулярной прецессии.
Резонансное соотношение частот 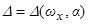 является медленно изменяющейся функцией, определяемой из уравнения вида
является медленно изменяющейся функцией, определяемой из уравнения вида
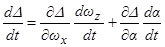 , (3.3)
, (3.3)
где 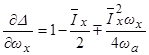 ,
, 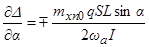 .
.
Правая часть уравнения (3.3) периодична по фазе 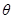 с периодом
с периодом 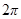 , следовательно, данное уравнение можно усреднить по
, следовательно, данное уравнение можно усреднить по 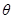 на нерезонансных областях движения.
на нерезонансных областях движения.
В результате усреднения получим:
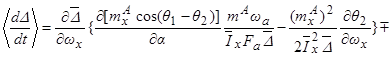
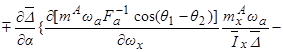
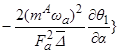 . (3.4)
. (3.4)
Выражение (3.4) применяется для записи условия внешней устойчивости резонанса 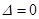 . Данное выражение может быть получено также следующим образом:
. Данное выражение может быть получено также следующим образом: 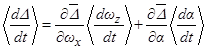 , где производные
, где производные 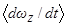 и
и 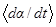 определяются из соответствующих усредненных уравнений ранее. Поэтому исследование внешней устойчивости резонансов при движении КА с малой асимметрией основывается на изучении нерезонансных эволюции медленных переменных при вторичных резонансных эффектах.
определяются из соответствующих усредненных уравнений ранее. Поэтому исследование внешней устойчивости резонансов при движении КА с малой асимметрией основывается на изучении нерезонансных эволюции медленных переменных при вторичных резонансных эффектах.
Введем в рассмотрение функцию Ляпунова: 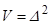 . Согласно работе [19] знак усредненной производной функции Ляпунова
. Согласно работе [19] знак усредненной производной функции Ляпунова 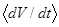 определяется знаками функции
определяется знаками функции 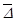 и производной
и производной 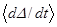 , так как
, так как 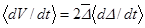 . При этом, знак функции
. При этом, знак функции 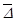 известен в каждой конкретной нерезонансной области, следовательно, внешняя устойчивость резонанса
известен в каждой конкретной нерезонансной области, следовательно, внешняя устойчивость резонанса 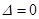 в системе (2.3)-(2.6) определяется знаком правой части уравнения (3.4).
в системе (2.3)-(2.6) определяется знаком правой части уравнения (3.4).
Относительно вида уравнения (3.4) можно сделать некоторые замечания. Так правую часть этого уравнения представляется в виде 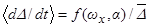 . При этом, уравнение (3.4) не содержит слагаемых с квадратами расстроек частот в знаменателях (члены
. При этом, уравнение (3.4) не содержит слагаемых с квадратами расстроек частот в знаменателях (члены 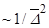 ), что нельзя сказать об усредненных уравнениях для медленных переменных
), что нельзя сказать об усредненных уравнениях для медленных переменных 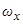 и
и 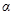 . Следовательно, внешнюю устой-чивость резонанса
. Следовательно, внешнюю устой-чивость резонанса 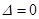 в уравнении (3.4) определяют члены вида
в уравнении (3.4) определяют члены вида 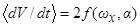 . Причём, знаки функции
. Причём, знаки функции 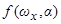 сохраняются для двух областей, прилегающих к одному и тому же резонансу. Поэтому, при динамически симметричном аппарате не может быть «полуустойчивых» резонансов, т.е. резонансов, «притягивающих» нерезонансные значения
сохраняются для двух областей, прилегающих к одному и тому же резонансу. Поэтому, при динамически симметричном аппарате не может быть «полуустойчивых» резонансов, т.е. резонансов, «притягивающих» нерезонансные значения 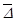 с одной стороны и «отталкивающие» их с другой. Термин «полуустойчивый» резонанс позаимствован из теории колебаний, где имеется термин полуустойчивый предельный цикл. Следовательно, резонанс в данном случае либо внешне устойчив при
с одной стороны и «отталкивающие» их с другой. Термин «полуустойчивый» резонанс позаимствован из теории колебаний, где имеется термин полуустойчивый предельный цикл. Следовательно, резонанс в данном случае либо внешне устойчив при 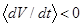 , либо внешне неустойчив при
, либо внешне неустойчив при 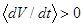 .
.
В таблице 3.1 представлены области внешней устойчивости (неустойчивости) главного резонанса 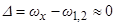 , соответствующие КА различным с различными видами асимметрии.
, соответствующие КА различным с различными видами асимметрии.
Таблица 3.1
| Вид асимметрии спускаемого аппарата | Вид внешней устойчивости главного резонанса | Условие внешней устойчивости | Область внешней устойчивости |
| Смещение центра масс и аэро- динамическая асимметрия | устойчив | 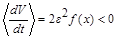
| 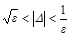
|
| Смещение центра масс и аэро- динамическая асимметрия | Неустойчив | 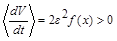
| 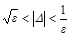
|
| Массово-инерционная и аэро-динамическая асимметрия | Устойчив | 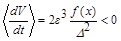
| 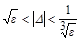
|
| Массово-инерционная и аэро-динамическая асимметрия | Неустойчив | 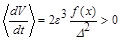
| 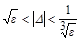
|
| Массово-инерционная и аэро-динамическая асимметрия | полу- устойчивый | 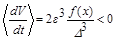 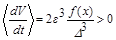
| 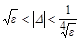
|
На рис.3.1-3.2 показаны, соответственно, области внешней устойчивости и внешней неустойчивости главного резонанса при 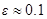 для динамически симметричного КА, построенные в соответствии с таблицей 3.1.
для динамически симметричного КА, построенные в соответствии с таблицей 3.1.
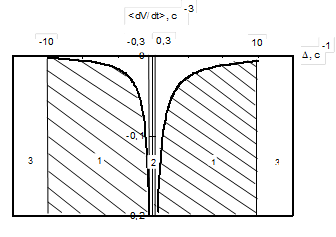 |
Рис. 3.1 - Области внешней устойчивости
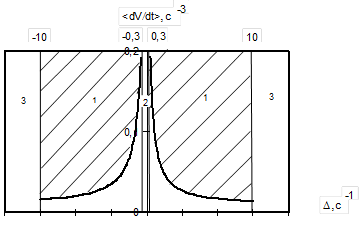 главного резонанса при
главного резонанса при 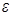 =0,1
=0,1
Рис. 3.2 - Области внешней неустойчивости главного резонанса при 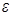 =0,1
=0,1
На рис.3.1 под цифрами 1 обозначены области внешней устойчивости резонанса, под цифрой 2 – область внутренней устойчивости резонанса, а цифрами 3 – области влияния возмущений, не приводящих к внешней устойчивости резонанса.
На рис. 3.2 под цифрами 1 обозначены области внешней неустойчивости резонанса, под цифрой 2 – область внутренней устойчивости резонанса, а цифрами 3 – области влияния возмущений, не приводящих к внешней устойчивости резонанса. Нижняя граница областей внешней устойчивости 1 по величине 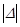 совпадает с границей резонансной зоны (порядка
совпадает с границей резонансной зоны (порядка 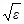 ).
).
На верхней границе областей внешней устойчивости по величине 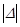 порядок малости производной
порядок малости производной 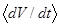 увеличивается на
увеличивается на 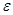 , поэтому внешней устойчивости здесь не наблюдается.
, поэтому внешней устойчивости здесь не наблюдается.
При малых углах атаки условие внешней устойчивости резонанса 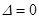 значительно упрощается, так как в этом случае
значительно упрощается, так как в этом случае 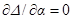 . Это условие принимает вид:
. Это условие принимает вид: 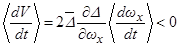 , где
, где 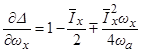 (
( 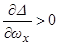 для вытянутых КА), а производная
для вытянутых КА), а производная 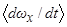 определяется из выражения (2.24). Следовательно, о внешней устойчивости (неустойчивости) главного резонанса при малых углах атаки можно судить по знаку обобщенного параметра асимметрии
определяется из выражения (2.24). Следовательно, о внешней устойчивости (неустойчивости) главного резонанса при малых углах атаки можно судить по знаку обобщенного параметра асимметрии 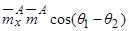 .
.
Представляет также интерес изучение эволюций медленных переменных в пространстве ( 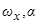 ,V). При этом, может быть выявлена полная картина эволюционных движений медленных переменных на нерезонансных областях, прилегающих к резонансам. Решение данной задачи основывается на получении усреднённых уравнений для переменных
,V). При этом, может быть выявлена полная картина эволюционных движений медленных переменных на нерезонансных областях, прилегающих к резонансам. Решение данной задачи основывается на получении усреднённых уравнений для переменных 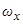 и
и 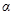 в нерезонансном случае. Рассмотрим рис.3.3, где в пространстве (
в нерезонансном случае. Рассмотрим рис.3.3, где в пространстве ( 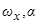 ,V) показаны нерезонансные эволюции медленных переменных в усреднённых уравнениях для переменных
,V) показаны нерезонансные эволюции медленных переменных в усреднённых уравнениях для переменных 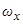 (
( 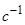 ) и
) и 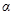 (град.). Причем, на рис.3.3 положительная ветвь резонансной кривой (
(град.). Причем, на рис.3.3 положительная ветвь резонансной кривой ( 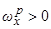 ) соответствует внешне устойчивому резонансу. Напротив, отрицательная ветвь (
) соответствует внешне устойчивому резонансу. Напротив, отрицательная ветвь ( 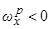 ) представляет эволюции медленных переменных при внешне неустойчивом резонансе.
) представляет эволюции медленных переменных при внешне неустойчивом резонансе.
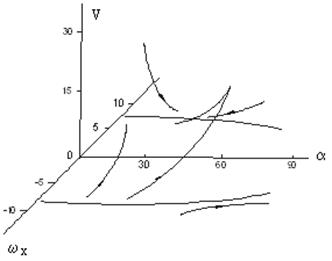
Рис.3.3 – Функция Ляпунова при эволюции
медленных переменных
Исходные данные для рис.3.3 соответствуют данным рис.3.1 и рис.3.2. Параллельно проводились также расчёты нерезонансных траекторий по исходным нелинейным уравнениям, подтверждающие справедливость полученных результатов. При этом оказалось, что при дальнейшем движении внешне устойчивый резонанс, показанный на рис.3.3, переходит во внутренне устойчивый резонанс.
Таким образом, получены условия внешней устойчивости или неустойчивости главного резонанса при движении на нерезонансных участках динамически симметричного КА в атмосфере.
Проанализируем внешнюю устойчивость главного резонанса 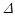 =0 для КА при
=0 для КА при 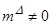 . Как и последнем параграфе данной главы, введем функцию Ляпунова
. Как и последнем параграфе данной главы, введем функцию Ляпунова 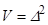 . Тогда условие внешней устойчивости главного резонанса имеет вид:
. Тогда условие внешней устойчивости главного резонанса имеет вид:
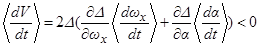 .
.
Напротив, если 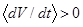 , то главный резонанс является внешне неустойчивым.
, то главный резонанс является внешне неустойчивым.
Внешнюю устойчивость главного резонанса рассмотрим на примере двух частных случаев, представленных ранее.
Второй частный случай. Сочетание массовой, аэродинамической и инерционной асимметрий при 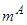 =0.
=0.
Знак производной 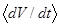 определяется знаком резонансной расстройки
определяется знаком резонансной расстройки 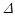 и знаком выражения
и знаком выражения 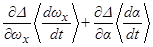 . В свою очередь, знак расстройки
. В свою очередь, знак расстройки 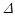 зависит от выбора нерезонансного участка движения СА. Знак выражения
зависит от выбора нерезонансного участка движения СА. Знак выражения 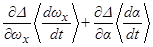 также зависит от знака расстройки
также зависит от знака расстройки 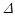 , а также от асимметрии аппарата.
, а также от асимметрии аппарата.
Анализируя производную функции Ляпунова 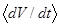 , в этом случае можно получить также условия того, чтобы резонанс
, в этом случае можно получить также условия того, чтобы резонанс 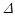 =0 являлся либо внешне устойчивым (при
=0 являлся либо внешне устойчивым (при 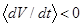 ), либо внешне неустойчивым (при
), либо внешне неустойчивым (при 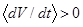 ) (при этом не реализуются внешне «полуустойчивые» резонансы). Для полуустойчивых резонансов характерны различные знаки производной
) (при этом не реализуются внешне «полуустойчивые» резонансы). Для полуустойчивых резонансов характерны различные знаки производной 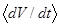 на двух нерезонансных участках прилегающих к одному резонансу (при
на двух нерезонансных участках прилегающих к одному резонансу (при 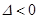 и
и 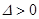 ). Следовательно, если на одном из таких участков, например
). Следовательно, если на одном из таких участков, например 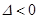 , наблюдается внешняя устойчивость, то на втором участке (
, наблюдается внешняя устойчивость, то на втором участке ( 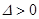 ) главный резонанс внешне неустойчив. Условие не реализации внешне «полуустойчивого» главного резонанса имеет вид:
) главный резонанс внешне неустойчив. Условие не реализации внешне «полуустойчивого» главного резонанса имеет вид:
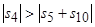 , (3.5)
, (3.5)
где 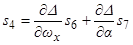 ,
, 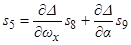 ,
,
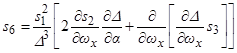 ,
,
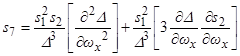 ,
, 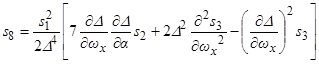 ,
,
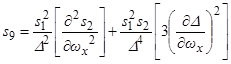 ,
, 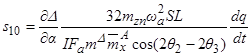 ,
, 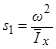 ,
,
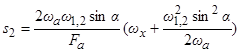 ,
, 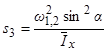 .
.
Напротив, при выполнении условия 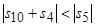 резонанс
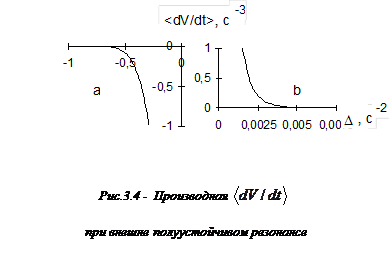
резонанс 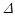 =0 является внешне полуустойчивым. На рис.3.4 и рис.3.5 изображаются производные функции Ляпунова при внешне полуустойчивом и внешне устойчивом резонансе, соответственно.
=0 является внешне полуустойчивым. На рис.3.4 и рис.3.5 изображаются производные функции Ляпунова при внешне полуустойчивом и внешне устойчивом резонансе, соответственно.
 | |||
|
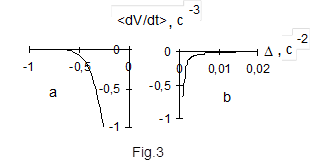 |
Рис.3.5 - Производная 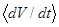
при внешне устойчивом резонансе
|
На рис.3.6 показаны эволюции медленных переменных 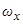 (
( 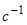 ) и
) и 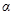 (град) в пространстве (
(град) в пространстве ( 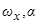 ,V) при полуустойчивых резонансах
,V) при полуустойчивых резонансах 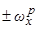 . При этом, если
. При этом, если 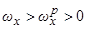 и резонанс
и резонанс 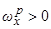 внешне устойчив, то при
внешне устойчив, то при 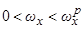 тот же резонанс является внешне неустойчивым. Аналогично, при
тот же резонанс является внешне неустойчивым. Аналогично, при 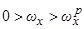 отрица-тельный резонанс
отрица-тельный резонанс 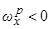 является внешне устойчивым, однако, при
является внешне устойчивым, однако, при 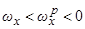 тот же резонанс уже внешне неустойчив.
тот же резонанс уже внешне неустойчив.
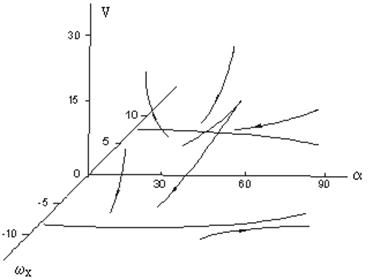
Рис.3.6 - Функция Ляпунова
при полуустойчивых резонансах
Данные об эволюциях угла атаки и угловой скорости 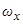 для построения рис.3.6 получены при численном интегрировании усредненных уравнений (2.29)-(2.30). При этих данных наблюдается выполнение условия
для построения рис.3.6 получены при численном интегрировании усредненных уравнений (2.29)-(2.30). При этих данных наблюдается выполнение условия 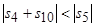 .
.
Итак, в первом частном случае возможна реализация как внешне устойчивого или неустойчивого, так и внешне полуустойчивого главного резонанса.
Третий частный случай. Сочетание аэродинамической и инерционной асимметрий в случае 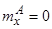 .
.
Знак производной 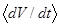 в этом случае также определяется знаком резонансной расстройки
в этом случае также определяется знаком резонансной расстройки 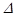 и знаком выражения
и знаком выражения 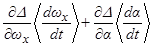 . Знак выражения
. Знак выражения 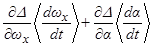 также зависит, как от знака резонансной расстройки
также зависит, как от знака резонансной расстройки 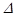 , так и от асимметрии КА. Только в данном случае - это уже другая асимметрия.
, так и от асимметрии КА. Только в данном случае - это уже другая асимметрия.
Анализируя производную функции Ляпунова 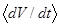 можно получить также условия того, что резонанс
можно получить также условия того, что резонанс 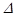 =0 является внешне устойчивым (при
=0 является внешне устойчивым (при 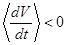 ) или внешне неустойчивым (при
) или внешне неустойчивым (при 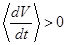 ). Это условие является условием не реализации полуустойчивого главного резонанса и имеет вид:
). Это условие является условием не реализации полуустойчивого главного резонанса и имеет вид:
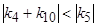 , (3.6)
, (3.6)
где 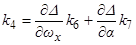 ,
, 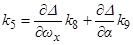 ,
,
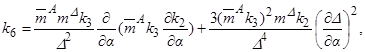
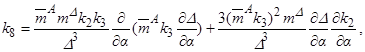
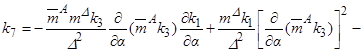
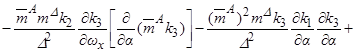
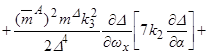
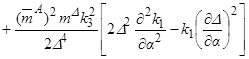 ,
, 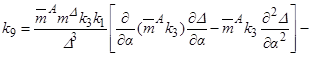
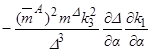
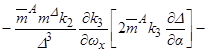
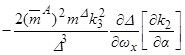 ,
, 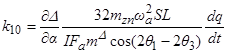 ,
, 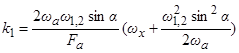 ,
,
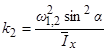 ,
, 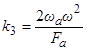 .
.
Напротив, при выполнении условия 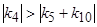 резонанс
резонанс 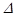 =0 является внешне полуустойчивым.
=0 является внешне полуустойчивым.
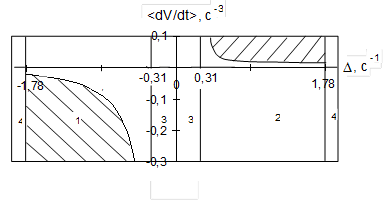
На рис.3.7-3.8 показаны, соответственно, области внешней устойчивости (неустойчивости) для полуустойчивого главного резонанса и области внешней устойчивости главного резонанса при 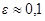 для динамически несимметричного КА, построенные в соответствии с таблицей 3.1. На рис.3.7 под цифрой 1 обозначена область внешней устойчивости резонанса, под цифрой 2 – область внешней неустойчивости резонанса, цифрами 3 – область внутренней устойчивости резонанса, а цифрами 4 – области влияния возмущений, не приводящих к внешней устойчивости резонанса. На рис.3.8 под цифрами 1 обозначены области внешней устойчивости резонанса, под цифрами 2 – область внутренней устойчивости резонанса, а цифрами 3 – области влияния возмущений, не приводящих к внешней устойчивости резонанса.
для динамически несимметричного КА, построенные в соответствии с таблицей 3.1. На рис.3.7 под цифрой 1 обозначена область внешней устойчивости резонанса, под цифрой 2 – область внешней неустойчивости резонанса, цифрами 3 – область внутренней устойчивости резонанса, а цифрами 4 – области влияния возмущений, не приводящих к внешней устойчивости резонанса. На рис.3.8 под цифрами 1 обозначены области внешней устойчивости резонанса, под цифрами 2 – область внутренней устойчивости резонанса, а цифрами 3 – области влияния возмущений, не приводящих к внешней устойчивости резонанса.
 | |||
| | |||
Рис. 3.7 – Области внешней устойчивости
полуустойчивого резонанса при ε=0,1
Дата добавления: 2021-10-28; просмотров: 464;

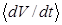 при внешне устойчивом резонансе
при внешне устойчивом резонансе










