Движение заряженных частиц в электрическом поле.

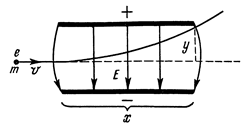
Пусть частица массой m и с зарядом e влетает со скоростью v в электрическое поле плоского конденсатора. Длина конденсатора x, напряженность поля равна Е. Смещаясь в электрическом поле вверх, электрон пролетит через конденсатор по криволинейной траектории и вылетит из него, отклонившись от первоначального направления на y. Под действием силы поля, F = eE = ma частица движется ускоренно по вертикали, поэтому 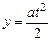. Время движения частицы вдоль оси ох с постоянной скоростью 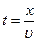. Тогда 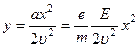. А это есть уравнение параболы. Т.о. заряженная частица движется в электрическом поле по параболе.

3. Движение заряженных частиц в магнитном поле.

Рассмотрим движение заряженной частицы в магнитном поле напряженностью Н. Силовые линии поля изображены точками и направлены перпендикулярно к плоскости рисунка (к нам).

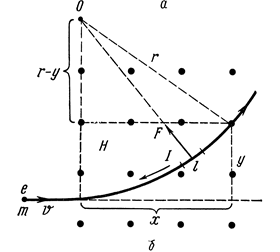
Движущаяся заряженная частица представляет собой электрический ток. Поэтому магнитное поле отклоняет частицу вверх от ее первоначального направления движения (направление движения электрона противоположно направлению тока)

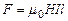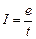Согласно формуле Ампера сила, отклоняющая частицу на любом участке траектории равна , ток , где t - время, за которое заряд e проходит по участку l. Поэтому 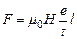. Учитывая, что 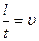, получим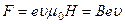

Сила F называется лоренцевой силой. Направления F, v и H взаимно перпендикулярны. Направление F можно определить по правилу левой руки.

Будучи перпендикулярна скорости 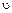, лоренцева сила изменяет только направление скорости движения частицы, не изменяя величины этой скорости. Отсюда следует, что:

1. Работа силы Лоренца равна нулю, т.е. постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей (не изменяет кинетической энергии частицы).

Напомним, что в отличие от магнитного поля электрическое поле изменяет энергию и величину скорости движущейся частицы.

2. Траектория частицы является окружностью, на которой частицу удерживает лоренцева сила, играющая роль центростремительной силы.

Радиус r этой окружности определим, приравнивая между собой лоренцеву и центростремительную силы:

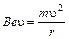, откуда .

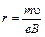Т.о. радиус окружности, по которой движется частица, пропорционален скорости частицы и обратно пропорционален напряженности магнитного поля.

Период обращения частицы T равен отношению длины окружности S к скорости частицы v: 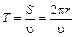. Учитывая выражение для r, получим 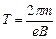. Следовательно, период обращения частицы в магнитном поле не зависит от ее скорости.

Если в пространстве, где движется заряженная частица, создать магнитное поле, направленное под углом 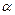к ее скорости 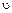, то дальнейшее движение частицы представит собой геометрическую сумму двух одновременных движений: вращения по окружности со скоростью 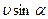в плоскости, перпендикулярной силовым линиям, и перемещения вдоль поля со скоростью 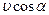. Очевидно, что результирующая траектория частицы окажется винтовой линией.

4. Электромагнитные счетчики скорости крови.

Принцип действия электромагнитного счетчика основан на движении электрических зарядов в магнитном поле. В крови имеется значительное количество электрических зарядов в виде ионов.

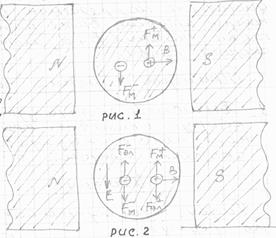
Предположим, что некоторое количество однозарядных ионов движется внутри артерии со скоростью 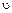. Если артерию поместить между полюсами магнита, ионы будут двигаться в магнитном поле.

Для направлений 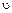и B, показанных на рис.1., магнитная сила 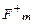, действующая на положительно заряженные ионы направлена вверх, а сила 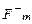, действующая на отрицательно заряженные ионы, направлена вниз. Под влиянием этих сил ионы движутся к противоположным стенкам артерии. Эта поляризация артериальных ионов создает поле E (рис.2), эквивалентное однородному полю плоского конденсатора. Тогда разность потенциалов в артерии U диаметром d связан с Е формулой 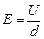. 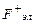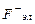Это электрическое поле, действуя на ионы, создает электрические силы и , направление которых противоположно направлению 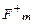и 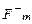, как показано на рис.2.

Концентрация зарядов на противоположных стенках артерии будет продолжаться до тех пор, пока электрическое поле не возрастет настолько, что = .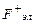

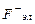Для состояния равновесия можно записать 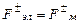; 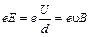, откуда .

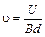Таким образом, скорость крови пропорциональна напряжению, возрастающему поперек артерии. Зная напряжение, а также значения B и d, можно определить скорость крови.