Теорема Дирихле о возможности перестановки местами членов ряда в сходящихся знакоположительных рядах.

Пусть 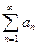- сходящийся знакоположительный ряд. Тогда его члены можно переставлять, менять местами, полученный ряд будет сходиться и иметь ту же сумму.

Доказательство. Проведем доказательство по индукции.

Пусть меняются местами два члена ряда 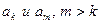. Тогда в исходном и полученном перестановкой членов ряде частичные суммы, начиная с 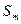будут совпадать. Следовательно, ряд, полученный перестановкой двух членов ряда, , будет сходиться и иметь ту же сумму.

Пусть при перестановке местами 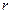членов ряда ряд сходится и имеет ту же сумму.

Пусть переставляются 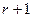членов ряда. Эта перестановка сводится к перестановке 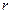членов ряда, а затем к перестановке еще какого-либо члена с каким-либо другим (перестановке двух членов ряда).

По индуктивному предположению при перестановке местами 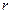членов ряда ряд сходится и имеет ту же сумму. Ряд, полученный перестановкой двух членов ряда, будет сходиться и иметь ту же сумму. Следовательно, и при перестановке 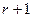членов ряда ряд будет сходиться и иметь ту же сумму.