Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора

Рассмотрим матричное однородное линейное дифференциальное уравнение

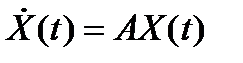(2.1.1)

Одним из методов численного решения дифференциальных уравнений является разложение решения на шаге h в ряд Тейлора [2.4] относительно предыдущего момента времени t

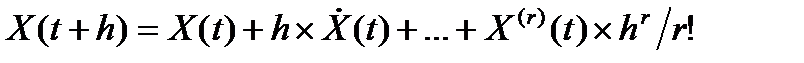(2.1.2)

Значения входящих в ряд Тейлора производных определим из уравнения (1):

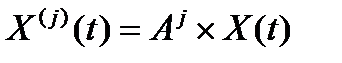, j = 1…r

Подставив эти значения в (2), получим:

X(t+h) = [I+Ah+A2h2/2…(Ah)r/r! …]X(t) (2.1.3)

eAh= [I+Ah+A2h2/2¼(Ah)r/r! …]

Матричный ряд в квадратной скобке представляет собой матричнуюэкспоненту:

(2.1.4)

Таким образом, точное решение уравнения (1) на шаге можно представить в виде:

X(t+h) = eAhX(t) (2.1.5)

При численном решении ряды в соотношениях (2), (3) и (4) усекаются. Порядком r метода численного решения называется максимальная степень шага h , оставляемая в разложении. Представим матричный экспоненциальный ряд в виде суммы:

eAh= eAh+ deAh, eAh= I+Ah+A2h2…(Ah)r/r! ,

(2.1.6)

deAh= (Ah)r+1/(r+1)! +…

где eAh- усеченная экспонента, deAh- отбрасываемая часть экспоненциального ряда (4).

Результат X(t+h) приближенного численного решения уравнения (1) на шаге h методом r -го порядка можно представить в следующем виде:

X(t+h) = [I+Ah+A2h2…(Ah)r/r!]X(t) = eAhX(t) (2.1.7)

Умножая матрицы (6) справа на X(t) с учетом (7), получим

X(t+h) = eAhX(t) = eAhX(t) + deAhX(t) = X(t+h) + dX(t+h) ,

(2.1.8)

где ошибка численного решения на шаге h или локальная ошибка метода

r -того порядка равна:

dX(t+h) = deAhX(t) = [(Ah)r+1/(r+1)! +…]X(t) (2.1.9)

Для приближенной оценки локальной ошибки можно использовать соотношение

dX(t+h) 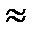[ (Ah)r+1/(r+1)! ]X(t)