Электростатическое экранирование

Понятие пространственного масштаба разделения зарядов можно уточнить, если рассмотреть электростатический потенциал вокруг отдельной заряженной частицы в плазме. В пустом пространстве вокруг частицы с зарядовым числом Z этот потенциал выражается как

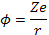(2.1)

Каждая заряженная частица вызывает поляризацию окружающей плазмы: вокруг такой частицы скапливается «атмосфера» с избытком частиц противоположного знака, экранирующая поле частицы. Экранированный потенциал может быть вычислен с помощью теории Дебая, развитой первоначально для растворов сильных электролитов. Эта теория основана на представлении о так называемом самосогласованном поле: находят такое распределение электрического поля, которое создает распределение частиц, возбуждающее в свою очередь заданное поле. Для нахождения самосогласованного поля используют уравнение Пуассона

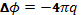(2.2)

и распределение Больцмана

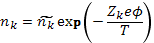(2.3)

где Т — температура в энергетических единицах; n_k — концентрация частиц с зарядовым числом Z_k в точке с по-потенциалом φ; 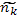— концентрация тех же частиц в точке с нулевым потенциалом (ее приравнивают средней концентрации по всему объему). Индексом k отмечены все частицы, включая электроны, которым приписывается Z = —1. В некоторых случаях удобно выделять электроны и нумеровать индексом i только ионы. Средние концентрации 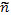удовлетворяют условию квазинейтральности

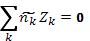(2.4)

или

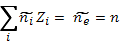(2.5)

где n — концентрация электронов. Объемный заряд

(2.6)

Подставив выражение (2.3) в уравнение (2.2), получим нелинейное уравнение самосогласованного поля в виде

(2.7)

Однако в таком нелинейном виде пользоваться уравнением не имеет смысла. Дело в том, что распределение Больцмана дает вероятность нахождения частицы в точке с потенциалом φ, т. е. среднее по времени значение концентрации, но мгновенные концентрации случайным образом меняются (флуктуируют) вокруг этого среднего значения, вызывая соответствующие флуктуации потенциала. Если в уравнении (2.7) под φ подразумевать среднее по времени значение потенциала, то окажется, что в правой части среднее значение функции заменено функцией от среднего значения, что допустимо только для линейных функций. Поэтому указанное уравнение может быть использовано только в линейном приближении. Для линеаризации раскладываем в правой части уравнения (2.7) экспоненциальные функции в ряд, сохраняя только линейные члены. Члены с нулевой степенью φ, согласно условию (2.4), взаимно уничтожаются, и получается линейное уравнение самосогласованного поля в виде

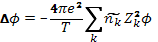(2.8)

Решение для сферически симметричного распределения потенциала вокруг точечного заряда имеет вид

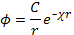(2.9)

где постоянная экранирования

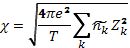(2.10)

Обратная величина называется длиной экранирования или дебаевской длиной. Легко видеть, что она полу чается из введенных выше пространственных масштабов разделения зарядов d_k по правилу сложения обратных квадратов:

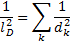(2.11)

Поэтому длину экранирования можно рассматривать как масштаб разделения зарядов или поляризационную длину для всей плазмы в целом. Постоянная С в выражении по-потенциала (2.9) должна быть такой, чтобы на малых расстояниях потенциал стремился к значению, определяемому формулой (2.1). Отсюда следует окончательное выражение для экранированного, или дебаевского, потенциала вокруг заряженной частицы в плазме

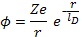(2.12)

Учитывая условие (2.5), удобно формулу (2.10) представить в виде

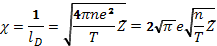(2.13)

где

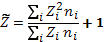(2.14)

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 1, §2)