Условие статической устойчивости системы источник–дуга
Дуговой разряд называется устойчивым, если он происходит непрерывно в течение достаточно длительного промежутка времени при заданных значениях тока и напряжения дуги. На устойчивость дуги оказывают влияние разнообразные факторы, которые могут быть отнесены к одной из двух категорий:
– факторы, обусловленные протеканием электрических, и тепловых процессов в приэлектродных областях и столбе дуги (величина напряжения источника, тока дуги, эмиссионная способность электродов, состав газовой атмосферы и т.п.);
– факторы, обусловленные свойствами электрической цепи, образующей систему источник питания–дуга.
Влияние физических факторов на возникновение и существование дугового разряда рассматривается в курсе «Теория сварочных процессов». Рассмотрим влияние на устойчивость дуги факторов второй категории.
Напомним, что система называется статически устойчивой, если случайное малое отклонение контролируемой величины с течением времени уменьшается, стремясь к нулю. В случае, если первоначальное малое отклонение постепенно нарастает, выводя систему из положения равновесия, мы имеет дело со статически неустойчивой системой. Понятие о статической устойчивости может быть проиллюстрировано на примере системы из шарика и криволинейной поверхности (рис. 1.7).
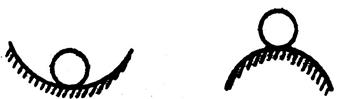
а) б)
Рис. 1.7. Модели статически устойчивой (а) и статически неустойчивой (б) систем
Пусть статическая ВАХ дуги и внешняя характеристика источника питания описываются некоторыми непрерывными, в рассматриваемом интервале токов и напряжений, функциями, которым соответствуют кривые Uд(I) и Uн(I) (рис. 1.8). Очевидно, что для случая, изображенного на рисунке, равновесие системы возможно в точках А и В, где Uи=Uд.
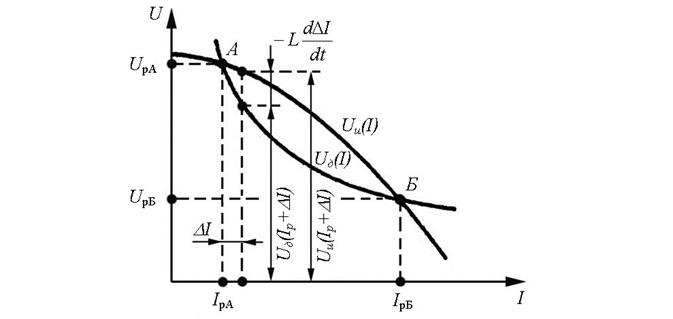
Рис. 1.8. Вольтамперная характеристика дуги Uд(I) и внешняя характеристика
источника Uи(I): А, Б – точки равновесия системы
Наша задача – определить, какое из этих положений равновесия является статически устойчивым.
В электрической схеме исследуемой системы (рис. 1.9) целесообразно в качестве отдельного элемента выделить индуктивность L, которую в явном или неявном виде содержат все реальные источники питания.

Рис. 1.9. Система источник питания–дуга
Если пренебречь активным сопротивлением цепи, ее электрическое состояние в любой момент времени может быть описано уравнением
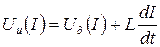 , (1.4)
, (1.4)
где 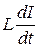 – ЭДС, наводимая в индуктивности при изменениях тока.
– ЭДС, наводимая в индуктивности при изменениях тока.
В точках равновесия 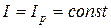 ,
, 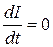 и
и 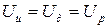 .
. 

Предположим, что в результате какого-либо внешнего воздействия (возмущения) ток в цепи отклонился на весьма малую величину ∆I . Тогда уравнение цепи примет вид
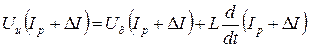 . (1.5)
. (1.5)
В общем случае характеристики дуги и источника нелинейны, однако для малых отклонений тока возможна их линеаризация, заключающаяся в замене реальных отрезков кривых касательным
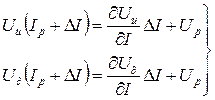 . (1.6)
. (1.6)
Подставив эти выражения в (2.2) и приняв во внимание, что 
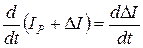 , получим
, получим
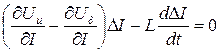 . (1.7)
. (1.7)
Решением дифференциального уравнения (1.7) является функция
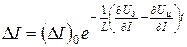 .
.
Нам уже известно, что частная производная 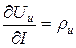 представляет собой дифференциальное сопротивление источника питания. Точно так же величина
представляет собой дифференциальное сопротивление источника питания. Точно так же величина 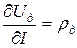 может быть определена как дифференциальное сопротивление дуги. Разность
может быть определена как дифференциальное сопротивление дуги. Разность
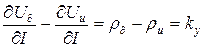
представляет собой дифференциальное сопротивление рассматриваемой системы, обычно называемое коэффициентом устойчивости. Тогда для изменения во времени отклонения тока окончательно получим
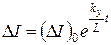 , (1.8)
, (1.8)
где (∆I)0 – постоянная интегрирования, представляющая собой начальное отклонение тока.
Анализ полученного выражения позволяет сделать вывод о том, что условием статической устойчивости нашей системы является положительный знак коэффициента Ку, т.е.
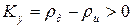 . (1.9)
. (1.9)
Действительно, при Kу > 0 показатель степени при числе e в (1.8) всегда отрицателен, поскольку L ≥ 0 , и ∆I монотонно уменьшается, стремясь к нулю (рис. 1.10).
Можно заметить, что статически устойчивому положению равновесия соответствует точка Б, где Ку > 0.
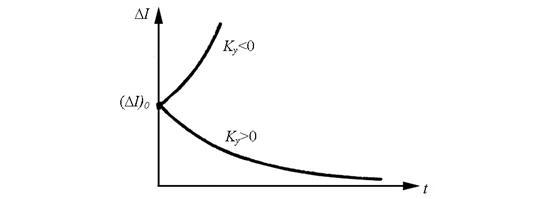
Рис. 1.10. Поведение системы в зависимости от знака коэффициента устойчивости
Если коэффициент устойчивости системы отрицателен, в соответствии с (1.8) первоначальное отклонение постепенно увеличивается, и система в исходное положение не возвращается.
Так, для точки А (рис. 1.8) любое случайное отклонение тока от значения IPA приводит к тому, что дуга либо погаснет (при ∆I0 < 0), либо перейдет в состояние, характеризующееся параметрами IPБ, UPБ (при ∆I0 > 0).
Поскольку крутизна ВАХ является естественным свойством дугового разряда и не может быть при заданных условиях сварки сколько-нибудь существенно изменена, единственным средством обеспечения статической устойчивости является выбор источника с требуемой внешней характеристикой.
В области малых токов дифференциальное сопротивление дуги отрицательно, и условие (1.9) обеспечивается только при питании дуги от источника с отрицательным же дифференциальным сопротивлением, причем необходимо, чтобы 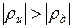 . Иначе говоря, для сварки малоамперной дугой необходимы источники с крутопадающими внешними характеристиками.
. Иначе говоря, для сварки малоамперной дугой необходимы источники с крутопадающими внешними характеристиками.
В подавляющем большинстве случаев сварку ведут на режимах, когда ВАХ дуги является жесткой, т.е. ее дифференциальное сопротивление близко к нулю. Статическая устойчивость такой дуги будет обеспечена также только при падающей внешней характеристике источника. Правда, в отличие от предыдущего случая, ограничений на абсолютную величину дифференциального сопротивления источника здесь не накладывается, поэтому принципиально пригодны источники как с круто-, так и с пологопадающими внешними характеристиками. В дальнейшем будет показано, что для всех видов дуговой сварки, где ВАХ дуги является жесткой, предпочтительнее источники с крутопадающими характеристиками.
На возрастающем участке ВАХ дуги статическая устойчивость может быть обеспечена при любых внешних характеристиках источника – падающих, жестких и даже возрастающих. По некоторым соображениям, не имеющим отношения к вопросу о статической устойчивости, при сварке дугами с возрастающими ВАХ применяют источники с пологопадающими или с почти жесткими внешними характеристиками.
Дата добавления: 2017-11-21; просмотров: 3116;











