УРАВНЕНИЕ ЭНЕРГИИ ГАЗОВОГО ПОТОКА

Процессы движения газа, происходящие в различных теплотехнических установках, связаны с преобразованием энергии в газовом потоке. Расчеты рабочих процессов этих установок строятся на общих положениях теории га­зового потока. Эта теория базируется на основных положениях термодина­мики и на ряде допущений, к числу которых относятся следующие:

1.Течение газа установившееся, т.е. в каждом выделенном сечении пара­метры газа во всех его точках остаются постоянными.

2.От сечения к сечению происходят бесконечно малые изменения пара­метров газа по сравнению со значениями самих параметров. Течение газа стационарное.

При таких допущениях газ при движении будет проходить ряд последова­тельных равновесных состояний.

Стационарное течение газа описывается системой уравнений, включаю­щей уравнение неразрывности потока, уравнение состояния и уравнение энергии (уравнение 1-го закона термодинамики применительно к газовому потоку).

Уравнение неразрывности характеризует неизменность массового расхо­да газа в любом сечении канала при установившемся течении. Это уравнение имеет вид

,

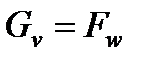или

,

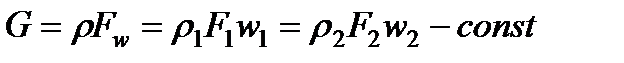где G - массовый секундный расход газа; 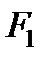, F₂ - площади поперечных сече­ний канала; w₁ , w₂ - скорости в соответствующих сечениях; ρ₁,ρ₂- плотности газа для тех же сечений потока (ρ=l/v).

Для одномерного газового потока в соответствии со вторым законом Ньютона (сила равна массе, умноженной на ускорение) можно записать сле­дующее соотношение [11]

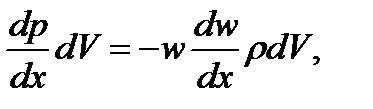
где

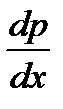- изменение давления по координате х;

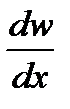- изменение скорости по координате х;

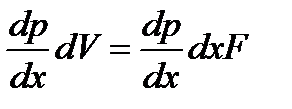- сила, действующая на выделенный элементарный объем dV;

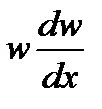- ускорение элементарной массы газа pdV.

Последнее соотношение можно переписать в виде

.

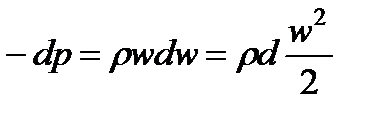Учитывая, что ρ=1/v, получим

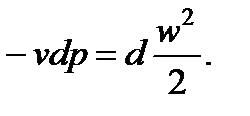(7.1)

Полученное соотношение показывает, что приращения давления dp и ско­рости dw имеют разные знаки. Следовательно, скорость одномерного потока возрастает с уменьшением давления.

Величина -vdp совпадает с формулой для располагаемой работы dl в уравнении первого закона термодинамики вида

.

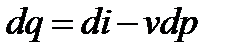Отсюда уравнение первого закона термодинамики для газового потока при отсутствии сил тяжести и сил трения в газе примет вид

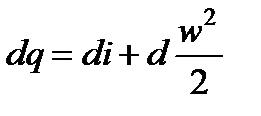, (7.2)

где 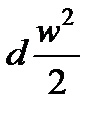приращение кинетической энергии газа на выделенном участке.

Так как 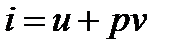, то

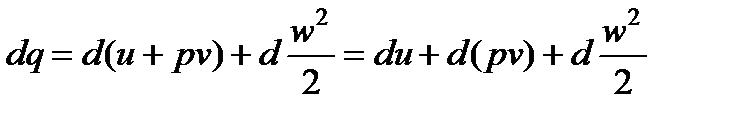, (7.3)

где d(pv) = pdv+ vdp- элементарная работа проталкивания.

Последнее уравнение показывает, что теплота, сообщаемая газу, затрачи­вается на изменение внутренней энергии, на работу проталкивания и на из­менение внешней кинетической энергии газа.

Уравнения (7.2),(7.3) являются основными для потоков газа и пара, при­чем они справедливы как для обратимых (не сопровождающихся действием сил трения), так и для необратимых течений (при наличии сил трения). При наличии сил трения должна затрачиваться работа трения l_тр, которая полностью переходит в теплоту q_тр. Вследствие равенства l_тр =q_тр обе эти величи­ны, имеющие противоположные знаки, взаимно сокращаются.

Уравнение (7.3) с учетом гравитационных сил принимает вид

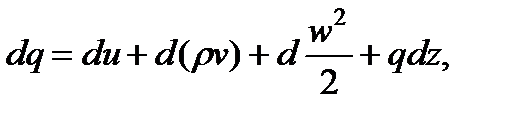
где gdz- элементарная работа против сил тяжести. Этой составляющей в га­зах ввиду ее малости обычно пренебрегают.

При адиабатном течении газа (dq=0)уравнение (7.2) принимает вид

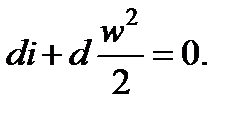(7.4)

После интегрирования получим

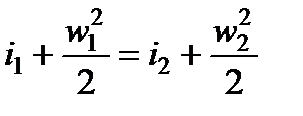(7.5)

Таким образом, при адиабатном течении газа сумма удельных энтальпии и кинетической энергии остается неизменной.

Отметим, что уравнения (7.2), (7.3), (7.4) справедливы в случае, когда газ при своем движении совершает лишь работу расширения и не производит полезной технической работы (например, работа на лопатках турбины и проч.). При совершении технической работы уравнение первого закона тер­модинамики (7.3) для потока газа примет вид

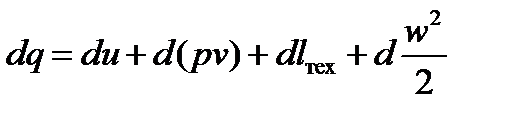, (7.6)

где dl_тех - элементарная техническая работа.

Сравнивая уравнение (7.5) с уравнением первого закона термодинамики (2.17) для расширяющегося, но не перемещающегося газа, получим

.

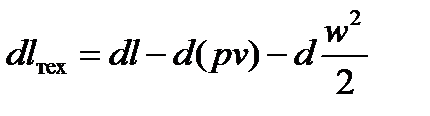Таким образом, техническая работа равна работе расширения газа за вы­четом работы проталкивания и работы, затрачиваемой на приращение кине­тической энергии газа.