РАСПОЛАГАЕМАЯ РАБОТА ГАЗОВОГО ПОТОКА

Соотношение (7.1) устанавливает равенство располагаемой работы dl₀= - vdp приращению кинетической энергии dw²/2 (при l_тех= 0). Это соот­ношение устанавливает основные особенности течения газа в каналах раз­личного профиля. Так, например, в конфузоре (сужающийся канал) происхо­дит уменьшение давления (dp<0) и увеличение скорости. Такие каналы называются соплами. В диффузорах (расширяющийся канал) течение газа сопровождается его сжатием с увеличением давления (dp >0) и уменьшением скорости (dw<0). Если сечение канала остается неизменным, то давление и скорости газа будут постоянными (dp=0, dw=0) и располагаемая работа dl₀=0.

Формулы для определения располагаемой работы в адиабатном и политропном процессах приведены соответственно в § 4.5, § 4.6.

При адиабатном течении газа формула (7.4), учитывая (7.1), примет вид dl₀= - di

После интегрирования получим

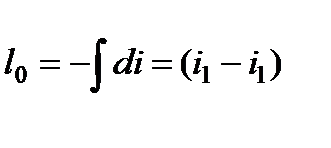(7.7)

Таким образом, при адиабатном течении располагаемая работа газа равна разности энтальпий в начальном и конечном состояниях.

§ 7.3. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПЛОВОГО И ДИФФУЗОРНОГО АДИАБАТНОГО ТЕЧЕНИЯ ГАЗА

Соплами называются каналы, в которых происходит снижение давления газа (dp<0), а диффузорами - каналы, в которых происходит повышение дав­ления газа (dp>0).

Из уравнения (7.1) следует, что знаки dp и dw противоположны. Поэтому всякий раз, когда давление в потоке понижается, скорость возрастает, а когда давление повышается, скорость убывает. Таким образом, в соплах происхо­дит разгон, а в диффузорах торможение потока. При конструировании про­точных частей энергетических устройств (турбин, компрессоров, реактивных двигателей и т. п.) практически важным является вопрос о том, какой про­филь должен иметь канал, чтобы обеспечить сопловое или диффузорное те­чение газа (т. е. разогнать или затормозить поток).

Некоторые качественные заключения могут быть сделаны на основе ана­лиза уравнения постоянства массового расхода G при стационарном течении газа

,

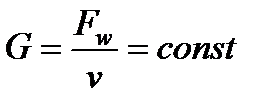где F - сечение канала.

Прологарифмировав это уравнение, а затем, продифференцировав, будем

иметь

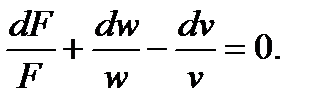(7.8)

Добавим к этому уравнению уравнение (7.1) и уравнение адиабаты в

дифференциальной форме

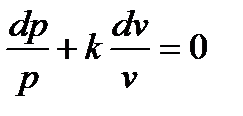. (7.9)

Это уравнение получается из уравнения pv^k =const, если последнее продиф­ференцировать, предварительно прологарифмировав.

Выразив из (7.1)

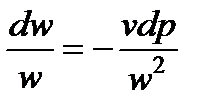
и из (7.9)

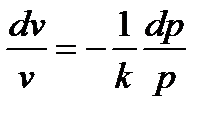
и подставив в (7.8), получим

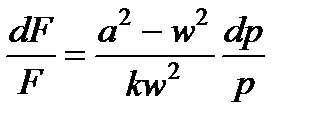, (7.10)

где 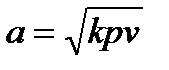- местная адиабатная скорость звука в газе, т.е. скорость рас­пространения малых упругих деформаций.

Если необходимо обеспечить сопловое течение (разгон потока) при ско­рости течения газа w меньше местной скорости звука а (с учетом того, что в соплах dp<0) из (7.10) имеем dF<0, т.е. канал должен быть суживающимся. Если же w>a (течение газа сверхзвуковое), из (7.10) получим dF>0, и для разгона потока сопло должно быть расширяющимся.

Для обеспечения диффузорного течения (торможения потока) при w<a (дозвуковое течение газа) из (7.10) с учетом того, что dp>0, получим dF>0, т.е. канал должен быть расширяющимся. Если же w>a ( течение газа сверх­звуковое) из (7.10) получим dF<0, и для торможения потока канал должен быть суживающимся. В случае течения несжимаемой жидкости v=const из

уравнения 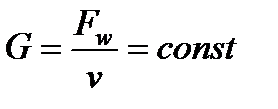получаем Fw=const . Поэтому для несжимаемой

жидкости увеличение сечения всегда ведет к торможению потока, а умень­шение сечения - к его разгону.