ИСТЕЧЕНИЕ ИДЕАЛЬНОГО ГАЗА ИЗ СУЖИВАЮЩИХСЯ СОПЕЛ
Допустим, что параметры газа на входе в сопло и выходе из него соответственно равны p1v1 и p2,v2, а площадь выходного сечения F2 (рис. 7.1). Скорость истечения газа из сопла может быть найдена путем интегрирования соотношения (7.1), записанного в виде
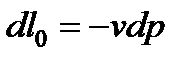 .
.
Интегрируя, получим
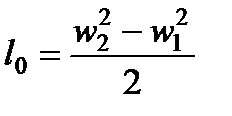 ,
,
где w1 и w2 - скорости газа на входе и на выходе из сопла.
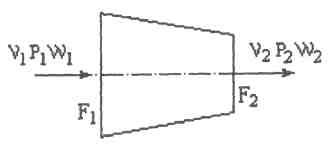
Рис. 7.1
В случае, когда w2>> w1 величиной w1 можно пренебречь. Тогда скорость на выходе из сопла w2=w будет
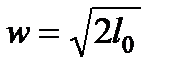 .
.
Подставляя в эту формулу значение располагаемой работы при обратимом адиабатном расширении газа (см. § 4.5), получим
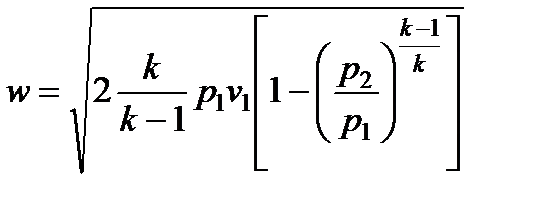 (7.11)
(7.11)
Используя формулу (7.7), находим еще одну формулу для w
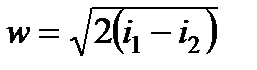
Расход газа находится по уравнению неразрывности
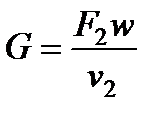 (7.12)
(7.12)
Выразим удельный объем v2 в выходном сечении сопла из уравнения адиабаты 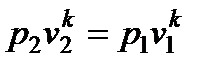
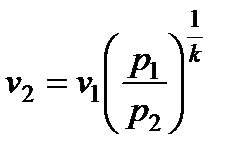 (7.13)
(7.13)
Подставляя (7.11), (7.13) в (7.12), получим
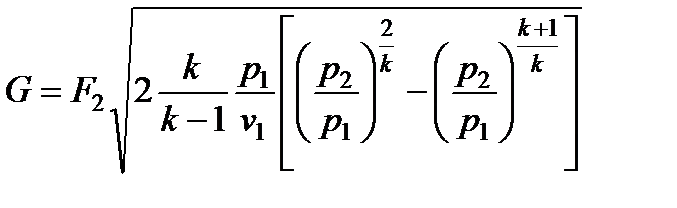 (7.14)
(7.14)
Если зафиксировать давление p1 и понижать давление за соплом р2, то скорость потока w2 и расход газа G будут увеличиваться. При достижении скорости w2 значения, равного значению местной скорости звука а, дальнейший разгон потока в суживающемся канале, как было показано в § 7.3, невозможен, поэтому после достижения давления р2 в устье сопла, равного давлению, при котором w2=a, расход газа G по мере понижения давления р2 будет оставаться неизменным и равным максимальному Gmax. Давление р2 , соответствующее достижению максимума расхода, называется критическим Р2кр ,отношение давлений p2кр /p1 также называется критическим.
Скорость истечения w2, равная местной скорости звука, называется критической скоростью и обозначается w2 кр.
Для получения максимального расхода при истечении газа из сопла необходимо взять первую производную по р2 от соотношения (7.14) и приравнять ее к нулю, т.е.
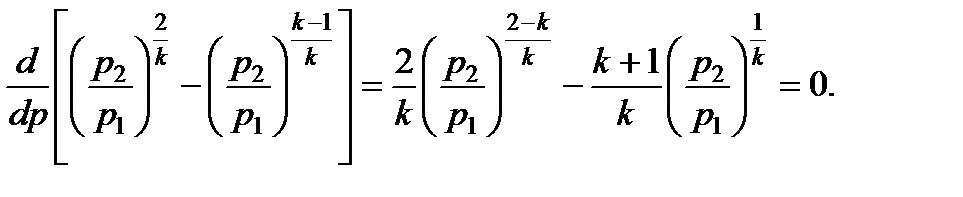
Отсюда
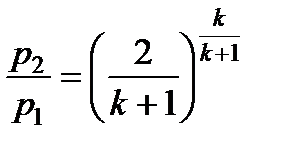 (7.15)
(7.15)
Это отношение давлений, обеспечивающее максимальный расход, называется критическим и обозначается через βкр
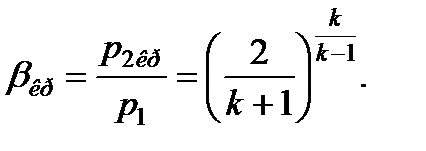
Критическое отношение давлений зависит только от свойств газов (от показателя адиабаты к). Например, для двухатомных газов k=1,4 и β= 0,528.
Подставляя в формулу (7.14) величину βкр , получим значение максимального расхода
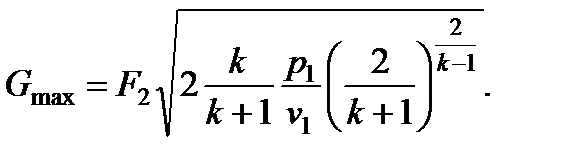 (7.16)
(7.16)
Подставляя величину βкр в формулу (7.11), получим формулу для критической скорости
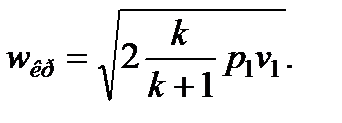 (7.17)
(7.17)
Критическая скорость истечения представляет собой максимальную скорость истечения газа из суживающегося сопла. Так как согласно приведенным выше рассуждениям максимальная скорость на выходе из сопла не может превысить местную скорость звука а, то, следовательно, wкр=a.
Из (7.13) и (7.15) следует
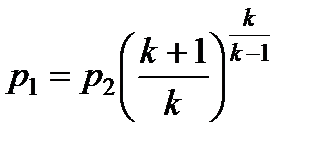 ;
;
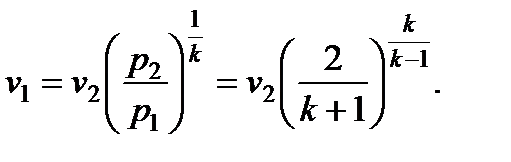
Подставляя p1 и v1 в (7.17), получим
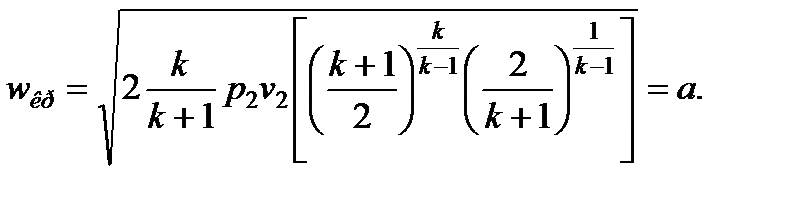
Скорость распространения звука определяется по формуле Лапласа
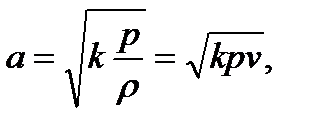
где р - давление среды; ρ- плотность; v - удельный объем.
Для идеального газа учитывая, что рv=RT, получим 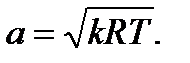
Дата добавления: 2016-06-05; просмотров: 3806;











