УРАВНЕНИЕ КЛАПЕЙРОНА - КЛАУЗИУСА

Вещество в зависимости от температуры и давления может находиться в твердой, жидкой и газообразной фазе.

Фазовым переходом называется процесс, сопровождающийся затратой теплоты и изменением объема, в котором происходит изменение агрегатного состояния вещества. Переход из одного агрегатного состояния в другое удоб­но рассматривать на рТ – диаграмме (рис.6.1)

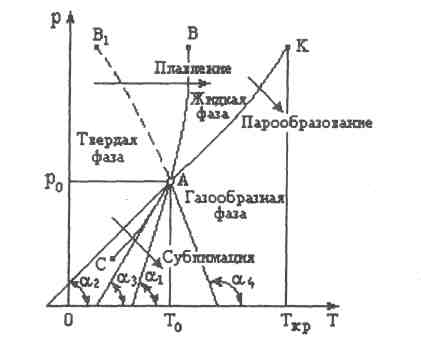
Рис. 6.1

Если в качестве независимого параметра взять температуру, то на рТ - диаграмме будут иметь место три характерные линии

; ; ;

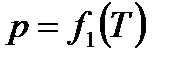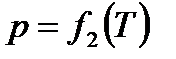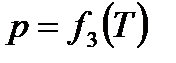Эти линии представляют собой геометрическое место точек, в которых находится в равновесном состоянии любая пара из трех агрегатных состоя­ний вещества.

Линия 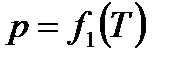(линия АК на рис.6.1.) соответствует равновесному со­стоянию жидкой и газообразной (парообразной) фаз. Эту линию еще назы­вают линией испарения (или по обратному процессу - линией конденсации).

Линия 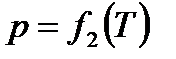(линия АС) соответствует равновесному состоянию твердой и газообразной фаз. Это линия сублимации (или по обратному процессу - десублимации).

На линии 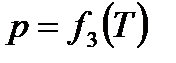(линия A В) находятся в равновесии твердая и жидкая фазы. Эта линия называется линией плавления (или по обратному процессу - затвердевания).

Переход из одного агрегатного состояния в другое при данной температу­ре будет происходить при строго определенных давлениях или при данном давлении при строго определенных температурах. Если, например, какое-либо вещество превращается из жидкого состояния в парообразное при оп­ределенном давлении, то его температура будет неизменной до тех пор, пока вся жидкость не превратиться в пар. Аналогичные процессы будут происхо­дить и на линиях плавления и сублимации.

Температура, при которой происходит переход вещества из твердого со­стояния в жидкое, называется температурой плавления (затвердевания). Ко­личество теплоты, отбираемое в этом процессе, называется теплотой плавле­ния (при затвердевании эта же теплота будет выделяться).

Температура перехода вещества из жидкого состояния в газообразное на­зывается температурой кипения (при данном давлении) или - температурой конденсации в обратном процессе. Количество теплоты, поглощаемое в этом процессе, называется теплотой парообразования (при конденсации это же количество теплоты будет выделяться).

Температура перехода вещества из твердого состояния в газообразное на­зывается температурой сублимации, а количество теплоты, подведенной в этом процессе, называется теплотой сублимации. Обратный переход - десублимация будет сопровождаться выделением этого же количества теплоты.

Кривая, на которой в зависимости от температуры и давления происходит переход из жидкого состояния в газообразное, заканчивается в точке К, на­зываемой критической точкой. В этой точке исчезает физическое различие между жидким и газообразным состоянием вещества. Обоснование наличия критической точки наиболее наглядно можно проследить на pV - диаграмме водяного пара (рис.6.2.).

Увеличение давления приводит к увеличению температуры кипения. При этом объем V газообразной фазы уменьшается, а объем жидкой фазы V возрастает. При некотором давлении (р=р_кр=22,12 МПа - для воды) эти два объема оказываются одинаковыми, что и наблюдается в критической точке, которой соответствует определенная для каждого вещества критическая тем­пература (для воды t_кр = 374,16 °С, см. § 6.3 ). Следовательно, в критической точке сухой пар имеет такую же плотность, что и кипящая вода и, таким об­разом, исчезает различие между жидкой и паровой фазами.

Все три кривые равновесного состояния различных фаз вещества пересе­каются в некоторой определенной для каждого вещества точке, называемой тройной точкой (точка А на рис.6.1.). В этой точке в термодинамическом равновесии находятся три различные фазы вещества - твердая, жидкая и га­зообразная, т.е. пропадает различие между этими тремя фазами.

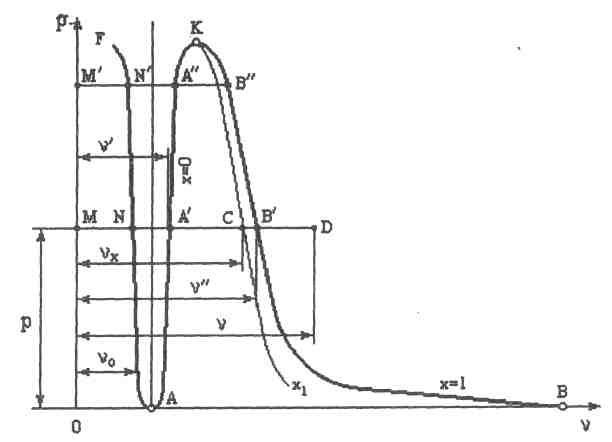
Рис. 6.2

Отметим некоторые особенности фазовых переходов.

Теплоемкость с_р в процессе фазового перехода равна бесконечности

,

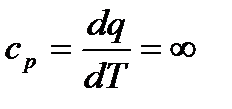так как ,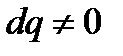

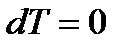
Коэффициенты изобарного (объемного) расширения α (2.12) и изотерми­ческого сжатия 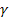равны бесконечности

; ,

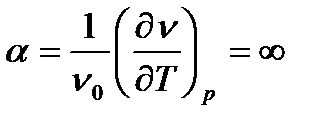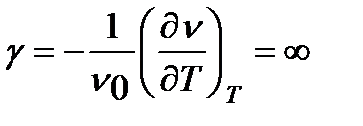так как ; ; .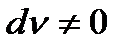

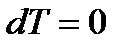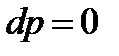Значительный интерес представляет уравнение Клапейрона-Клаузиуса, связывающее термические величины (температура, давление, удельный объ­ем) с калорическими (теплота фазового перехода). Это уравнение имеет вид (вывод см. в [13])

,

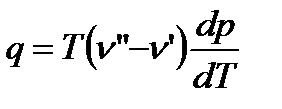где q - теплота фазового перехода; 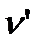- удельный объем жидкости или твердо­го тела; 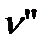- удельный объем пара; dp/dT - производная от давления по тем­пературе, взятая на кривой фазового перехода.

Уравнение Клайперона - Клаузиуса может быть применено ко всем изме­нениям агрегатного состояния веществ. В общем виде оно характеризует изменение давления фаз, находящихся в равновесии, от температуры. Но фи­зический смысл входящих в это уравнение величии в каждом отдельном слу­чае различен.

В случае плавления твердого тела (кривая АВ на рис. 6.1) величины из уравнения Клайперона-Клаузиуса будут иметь следующий физический смысл: q - удельная теплота плавления; 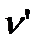- удельный объем твердого тела; 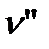- удельный объем жидкости. В случае газообразования (кривая АК): q - удельная теплота парообразования; 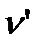- удельный объем кипящей жидкости;
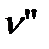- удельный объем сухого насыщенного пара.

При сублимации (кривая
AC): q - удельная теплота сублимации; 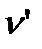- удельный объем твердого тела; 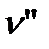- удельный объем сухого насыщенного пара.

С помощью уравнения Клапейрона - Клаузиуса можно установить наклон линий плавления, испарения и сублимации в тройной точке. Запишем это уравнение в виде

.

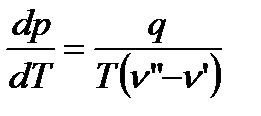Так как величины q, T, 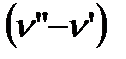для всех веществ всегда положительны (за исключением воды ввиду ее аномальности), то

.

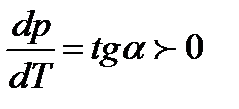Отсюда следует, что утлы наклона α₁, а₂, а₃ касательных кривых АВ, АК и АС в точке А к оси Т будут меньше 90° (рис.6.1).

Для воды вследствие ее аномальности объем воды в момент фазового пе­рехода меньше объема льда 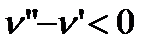. Поэтому величина dp/dT из уравнения Клайперона - Клаузиуса будет отрицательной и следовательно угол наклона α₄ кривой плавления льда (кривая АВ₁) будет больше 90°.

Таким образом, для всех нормальных жидкостей 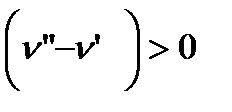и все линии фазовых превращений отклоняются вправо. Для воды кривая AB₁ равновес­ного состояния твердой и жидкой фаз с повышением давления отклоняется в сторону меньших температур (влево).

§ 6.3. pν- ДИАГРАММА ВОДЯНОГО ПАРА

На рис. 6.2. представлена фазовая pν - диаграмма, которая представляет собой график зависимости удельного объема воды и водяного пара от давле­ния (см.§ 2.5).

Кривая AF представляет зависимость удельного объема воды от давления при температуре

t = 0° С, т.е. это есть изотерма воды при нулевой темпера­туре. Область, заключенная между этой изотермой и осью ординат, является областью равновесного сосуществования жидкой и твердой фаз. Кривая AF почти параллельна оси ординат, так как вода практически несжимаемая жидкость. Поэтому удельный объем 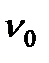воды в процессе сжатия изменяется незначительно.

При нагреве воды при некотором постоянном давлении p удельный объем будет увеличиваться и при достижении температуры кипения в точке А' удельный объем 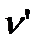жидкости становится максимальным. С увеличением дав­ления температура кипения возрастает и удельный объем 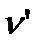в точке А" будет больше, чем в точке А'.

Зависимость удельного объема 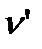от давления на pv - диаграмме изобра­жается кривой АК, называемой пограничной кривой жидкости. Всюду на этой кривой степень сухости х=0.

Дальнейший подвод к жидкости теплоты при неизменном давлении при­водит к процессу парообразования (линия А' В'), который заканчивается в точке В'. Пар в этой точке будет сухим насыщенным с удельным объемом 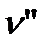Процесс А'В' является одновременно изобарным и изотермическим.

Зависимость удельного объема 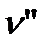от давления представлена кривой KB, которая называется пограничной кривой пара. На этой кривой степень сухо­сти х=1.

Если в состоянии, характеризуемом точкой В' (или В" при большем дав­лении), к пару подводить теплоту, то его температура и удельный объем бу­дут увеличиваться. Линия В'Д представляет процесс перегрева пара.

Таким образом, кривые АК и KB делят область диаграммы на три части. Левее кривой АК расположена область жидкости. Между кривыми АК и KB расположена область двухфазной системы, включающей пар и жидкость (пароводяная смесь). Правее кривой KB и выше точки К расположена об­ласть перегретого пара.

Точка К называется критической точкой (см. §2.5 и §6.2). Параметры критической точки для воды: t_к= 374,16⁰ С; 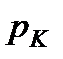= 22,12 МПа; 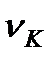= 0,0032 м³/кг; i_к= 2095,2 кДж/(кг^.К).

Точка А характеризует состояние кипящей жидкости в тройной точке (см. § 6.2). Температура кипения воды в этой точке t₀ = 0,001°С ≈ 0°С. Если в со­стоянии, характеризуемом тройной точкой, к жидкости подводить теплоту, то процесс кипения будет происходить по изобаре являющейся одновременно нулевой изотермой, которая при выбранном масштабе изображения кривых практически совпадает с осью абсцисс.

Между кривыми х=0и х=1расположены кривые промежуточных степе­ней сухости. Все они исходят из точки К.Одна из таких кривых со степенью сухости 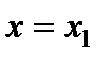приведена на рис. 6.2.

Удельное количество работы 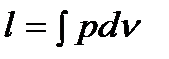, полученной в процессе или цикле, на pv - диаграмме изображается соответствующей площадью под кривой процесса или внутри цикла (см. рис. 6,7а, 6,8а, 6,9а).

§ 6.4. Ts - ДИАГРАММА ВОДЯНОГО ПАРА

Процесс нагрева воды от 0,01°С = 273,16 К до температуры кипения при давлении p₁-const характеризуется линией АаA₁. Линия А₁В₁является про­цессом парообразования и линия В₁Д₁- процессом перегрева пара (рис. 6.3.). Если нанести на Ts - диаграмме ряд таких изобарных процессов и соединить точки, в которых начинается и заканчивается процесс кипения, то получим две пограничные кривые АК - кривая начала кипения (х=0) и KB - кривая окончания кипения (кривая сухого пара x=1), которые сходятся в критиче­ской точке К.

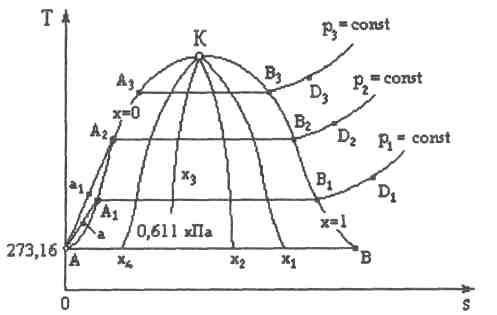
Рис. 6.3

Точка А здесь является тройной точкой (см. § 6.2,6.3) которой соответст­вует изобара

Р₀=0,611кПа и изотерма t₀=0,01° С =273,16 К.

Пограничные кривые АК и KB делят область диаграммы на три части. Левее кривой АК расположена область жидкости. Между кривыми АК и ВК -область влажного пара (пароводяной смеси). Правее кривой KB и выше точ­ки К находится область перегретого пара. Кривая АК берет свое начало в тройной точке А, расположенной на оси ординат, т.е. считается, что удельная энтропия при температуре 273,16°С близка к нулю. Изобары нагрева воды АаА₁, Аа₁А₂до температуры кипения соответственно при давлениях р₁и р₂даны как для нормальной жидкости, т.е. без учета аномальности воды, имеющей максимальную плотность при температуре t =4° С. Это допущение незначительно влияет на точность при расчетах. Давлению в тройной точке

р = 0,611кПа соответствует изобара АВ.

Между кривыми АК и KB нанесены кривые промежуточных степеней су­хости х₁, x₂, x_з, x₄, все эти кривые сходятся в критической точке К,где исче­зает различие между жидкой и паровой фазами, т.е. сухой пар и кипящая во­да имеют одинаковую плотность.

Удельное количество теплоты 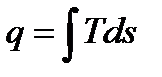, сообщаемое рабочему телу, на Ts - диаграмме изображается площадью под кривой процесса (см. рис. 6.6б, 6.7б, 6.8б). Удельная работа обратимого цикла l = q₁-q₂также может быть найдена в виде площади цикла. Таким образом, с помощью Ts - диаграммы достаточно просто можно найти термический кпд 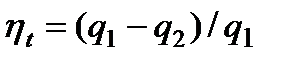обратимого цикла.

Удобство Ts - диаграммы в том, что она позволяет проследить изменение температуры рабочего тела и находить количество теплоты, участвующее в процессе. К неудобствам диаграммы следует отнести необходимость измере­ния соответствующих площадей. Ts - диаграмма широко применяется при исследовании паросиловых и холодильных установок, обеспечивая наиболее наглядное изображение процессов.

§6.5. iS - ДИАГРАММА ВОДЯНОГО ПАРА

is - диаграмма является наиболее удобной для расчетных целей. Это свя­зано с тем, что удельные количества теплоты и работы изображаются не площадями, как это имеет место в Ts- и pv - диаграммах, а отрезками линий (рис.6.4).

За начало координат в is - диаграмме принято состояние воды в тройной точке, где s₀=0 (допущение) i_o=0. По оси абсцисс откладывается удельная энтропия, а по оси ординат - удельная энтальпия. На основе данных таблиц водяного пара на диаграмму наносятся пограничные кривые жидкости (АК) и пара (KB) (соответственно нулевой х=0и единичной х=1степени сухости), сходящиеся в критической точке К. Пограничная кривая жидкости выходит из начала координат.

Изобары (p=const)в области влажного пара являются прямыми наклон­ными линиями, берущими начало на пограничной кривой нулевой степени сухости, к которой они касательны. В этой области изобары и изотермы сов­падают, т.е. они имеют одинаковый коэффициент наклона к оси абсцисс. Для любой изобары - изотермы

,

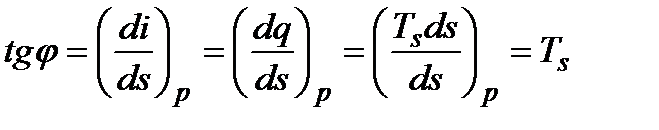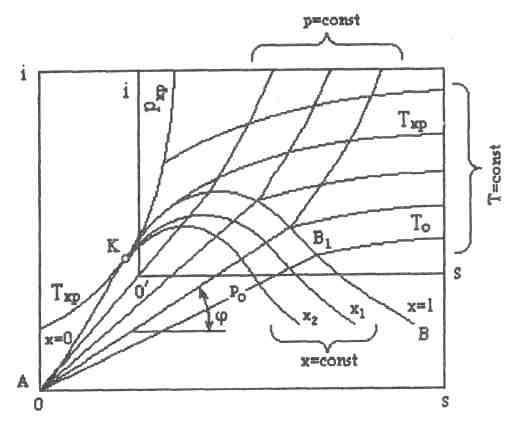
Рис. 6.4

где φ- угол наклона изобар к оси s, T_s - температура насыщения, неизменная для данного давления всюду между пограничными кривыми AК и КВ.

В области перегретого пара (правее и выше кривой х=1) изобары имеют вид кривых отклоняющихся вверх с выпуклостью, направленной вниз. Изо­термы в этой области отклоняются вправо и их выпуклость направлена вверх. Изобара АВ₁соответствует давлению в тройной точке р₀⁼0,000611 МПа. Область диаграммы, расположенная ниже тройной точки, характери­зует различные состояния смеси пара и льда.

Между кривыми АК и KB наносится сетка линий постоянной степени су­хости (x=const)пара, сходящихся в критической точке К.

Кроме того, на диаграмму наносится сетка изохор, имеющих вид кривых, поднимающихся вверх (как в области влажного, так и в области перегретого пара) более круто, чем изобары. На is -диаграмме рис. 6.3. изохоры не при­ведены.

В практических расчетах обычно используется лишь область диаграммы, расположенная в правом верхнем углу. В связи с чем, начало координат пе­реносится из точки 0 в точку 0', что дает возможность изображать диаграмму в большем масштабе.

Диаграмма is широко применяется для расчета процессов с водяным па­ром. Общий метод состоит в следующем.

1. По заданным начальным параметрам, характеристике процесса и за­данному конечному параметру в is-диаграмме находится график процесса.

2. По начальной и конечной точкам процесса находятся все основные па­раметры пара в этих точках.

3.Определяется изменение внутренней энергии по формуле

.

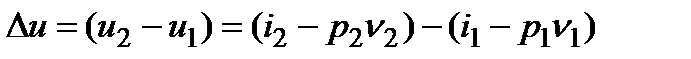4.Определяется теплота процесса по формулам:

а) процесс ν = const ;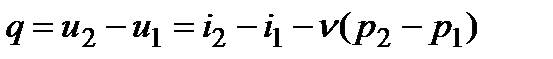

б) процесс р = const ;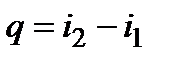

в) процесс Т = const ;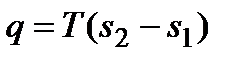

г) процесс s = const q = 0.

5.0пределяется удельная работа по формуле

.

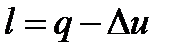Все рассмотренные выше диаграммы в pv-, Ts- и is- координатах в соот­ветствующих масштабах строятся на основе таблиц параметров, полученных из опытных и теоретических данных. Наиболее точные таблицы для водяно­го пара разработаны в Московском энергетическом институте под руково­дством проф. М.П.Вукаловича [9, 16].