Приведение моментов и сил сопротивления, инерционных масс и моментов инерции
2.2.1. Активные и реактивные моменты сопротивления.
В общем случае статический момент
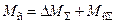 ,
,
где 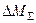 – суммарные потери в приводе;
– суммарные потери в приводе; 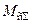 - суммарный статический момент.
- суммарный статический момент.
Обычно первая составляющая имеет сравнительно малую величину. Поэтому рассмотрим вторую составляющую статического момента, оказывающего наибольшее влияние на привод.
Для электропривода имеет значение, как зависит статический момент нагрузки от скорости. Такую зависимость описывает механическая характеристика механизма, то есть зависимость статического момента нагрузки от скорости 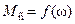 или
или 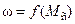 .
.
По характеру взаимодействия с электроприводом все силы и моменты делятся на две большие группы: активные и реактивные.
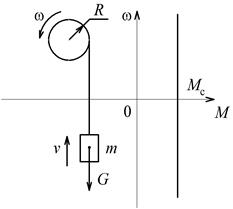
Активными силами и моментами называются силы и моменты, создаваемые внешними по отношению к двигателю источниками механической энергии и не зависящие от работы двигателя. Например, силы тяжести, ветровые нагрузки. Активный статический момент не меняет своего знака при изменении направления вращения.
| 
|
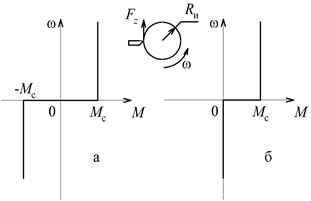
| Рис. 2.2. Механическая характеристика активного момента | Рис. 2.3. Механическая характеристика реактивного момента |
На рис.2.2. приведенный момент силы тяжести груза G:
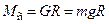 ,
,
где g – ускорение свободного падения; m – масса груза.
Реактивными силами и моментами называются силы и моменты, возникающие как реакция на момент, создаваемый двигателем и направлены против направления вращения двигателя. Все реактивные силы и моменты зависят от скорости. По характеру этой зависимости ( 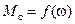 ) различают нагрузки типа сухого трения, типа вязкого трения и вентиляторного типа.
) различают нагрузки типа сухого трения, типа вязкого трения и вентиляторного типа.
Силы и моменты сухого трения неизменны по модулю, но скачком изменяют направление в зависимости от знака скорости
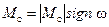 .
.
Характеристика момента сухого трения показана на рис. 2.3, a.
Реактивные нагрузки, возникающие при различных технологических процессах обработки, могут иметь одно направление, скачком изменяя своё значение до нуля при изменении знака скорости. Примером может служить зависимость (рис. 2.3, б) момента резания от скорости при обработке изделия резцом. Значение статического момента при этом пропорционально усилию резания 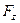 :
:
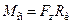 ,
,
где 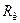 – радиус изделия.
– радиус изделия.
Силы и моменты вязкого трения линейно зависят от скорости (рис. 2.4, а):
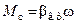 ,
,
где 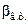 – коэффициент пропорциональности.
– коэффициент пропорциональности.
Обычно момент вязкого трения составляет 8-10% от момента сухого трения.
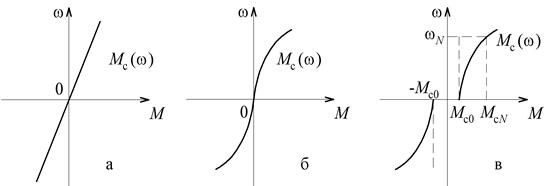
Третий тип часть встречающихся нагрузок – вентиляторная нагрузка. Такая нагрузка зависит от скорости в более высокой степени (рис. 2.4, б)
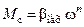 ,
, 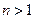 .
.
При 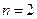 нагрузку называют чисто вентиляторной. Такой зависимостью обладают центробежные вентиляторы. Для ряда механизмов показатель степени
нагрузку называют чисто вентиляторной. Такой зависимостью обладают центробежные вентиляторы. Для ряда механизмов показатель степени 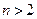 . Такую характеристику имеют центробежные насосы, работающие на противодавление.
. Такую характеристику имеют центробежные насосы, работающие на противодавление.
В реальности у механизма есть некоторый начальный момент трогания 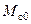 , составляющий 20-40% от номинального
, составляющий 20-40% от номинального  (рис. 2.4, в).
(рис. 2.4, в).
Существуют механизмы циклического действия, у которых момент нагрузки зависит от угла поворота:
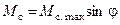 .
.
Рассмотренные типовые нагрузки обычно содержатся в качестве составляющих в нагрузках реальных электроприводов.
|
| Рис. 2.4. Моменты нагрузки типа вязкого трения (а), вентиляторного (б) и реального вентиляторного типов (в) |
2.2.2. Приведение момента инерции для вращательного и поступательного движения рабочего органа
Условием соответствия приведенной расчетной схемы реальной механической системе является выполнение закона сохранения энергии. При приведении необходимо обеспечить сохранение запаса кинетической и потенциальной энергии системы, а так же элементарной работы всех действующих в системе сил и моментов на возможных перемещениях. Поэтому при приведении моментов инерции элемента системы, движущегося вращательно со скоростью 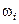 или массы, поступательно движущейся со скоростью
или массы, поступательно движущейся со скоростью 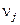 к расчетной скорости
к расчетной скорости 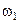 должны выполняться условия
должны выполняться условия
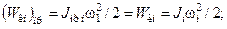
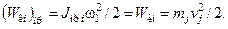
Отсюда можно получить формулы приведения моментов инерции:
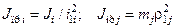 ,
,
где 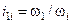 – передаточное число от вала приведения до i-го вала;
– передаточное число от вала приведения до i-го вала; 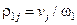 – радиус приведения к валу со скоростью
– радиус приведения к валу со скоростью 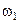 .
.
| 
|
| а | б |
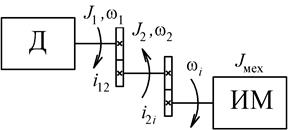
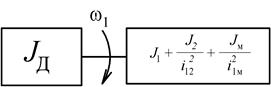
| Рис. 2.5. Расчетная (а) и эквивалентная расчетная (б) схемы механической части (вращательное движение рабочего органа) | |
| 
|
| а | б |
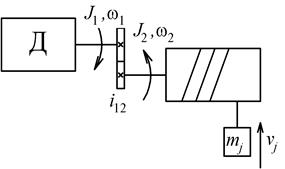
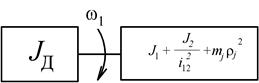
| Рис. 2.6. Расчетная (а) и эквивалентная расчетная (б) схемы механической части (поступательное движение рабочего органа) |
Приведенный суммарный момент инерции для механизма на рис 2.5, а вычисляется с учетом формул приведения для моментов инерции следующим образом:
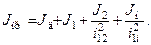
В случае поступательного движения рабочего органа исполнительного механизма:
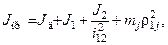
где 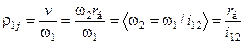 - радиус приведения.
- радиус приведения.
2.2.3. Приведение моментов сопротивления
Приведение моментов сопротивления от одной оси вращения к другой может быть произведено на основании энергетического баланса системы. Потери мощности, возникающие в промежуточных передачах, учитываются введением в расчеты соответствующего КПД - 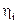 .
.
Без учета КПД передачи приведение моментов сопротивления можно выполнить приравниванием мощностей на двигателе и рабочем органе ИМ:
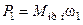 и
и 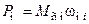 ,
,
где 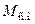 – момент сопротивления производственного механизма.
– момент сопротивления производственного механизма.
Откуда статический момент на валу двигателя
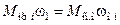 ,
, 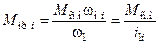 .
.
Приведение сил сопротивления производится аналогично приведению моментов. Без учета потерь в передаче приведенный к валу двигателя статический момент
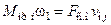 ,
, 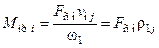 .
.
2.2.4. Об учете КПД передаточного механизма
Рассмотрим упрощенную схему механической части электропривода. Передаточный механизм (ПМ) обладает двумя характеристиками передаточное число 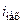 и КПД
и КПД 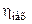 механизма. В КПД механизма входят все КПД элементов
механизма. В КПД механизма входят все КПД элементов
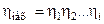 .
.
Двигатель создает механическую мощность, направленную от сети к исполнительному механизму. Уравнение баланса мощностей
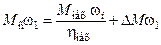 , (1.1)
, (1.1)
где 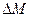 – момент потерь, складывающийся из момента трения в двигателе и передачах.
– момент потерь, складывающийся из момента трения в двигателе и передачах.
Величина момента потерь редко превосходит 3-5 % от номинального момента и им часто пренебрегают, считая 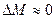 .
.
Разделив обе части уравнения (1.1) на 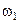 , получим
, получим
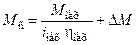 ,
,
где 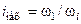 - общее передаточное число передаточного механизма.
- общее передаточное число передаточного механизма.
Таким образом, для двигательного режима справедлива следующая формула для определения приведенного статического момента:
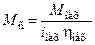 .
.
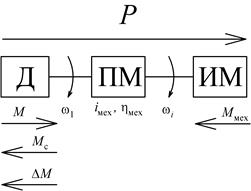
Рис. 2.7, а иллюстрирует направления потока энергии и моментов.
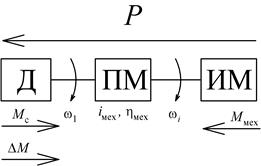
В генераторном режиме источником момента является сам исполнительный механизм. Статическим моментом в данном случае является момент двигателя в тормозном режиме. Уравнение баланса энергий для генераторного режима
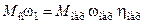 .
.
Выполнив процедуру деления на скорость двигателя, получаем
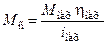 .
.
При поступательном движении статический момент в двигательном режиме
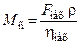 ,
,
в генераторном режиме
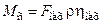 .
.
| 
|
| а | б |
| Рис. 2.7. Направления энергии и моментов для двигательного (а) и генераторного (б) режимов работы привода |
Дата добавления: 2017-11-21; просмотров: 1844;











