Время ускорения и замедления привода

Время переходных режимов привода: пуска, торможения, перехода от одной скорости к другой влияет на производительность механизма. Определение времени переходных процессов основано на интегрировании уравнения движения привода. Разделяя переменные, получим:

.

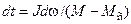Время переходного режима при изменении скорости от 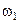до

.

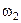
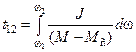Если принять, что 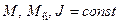, результатом решения интеграла будет

.

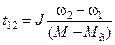Рассчитаем время пуска привода от состояния покоя ( 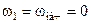) до номинальной скорости 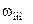с пусковым моментом 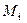при наличии на валу двигателя момента сопротивления 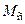(см. рис. 2.10)

.

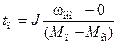Если требуется точно рассчитать время переходного процесса для привода с асинхронным двигателем ( 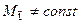), то следует использовать формулу в интегралах.

Теоретически, полное время переходного процесса равно бесконечности. Поэтому в практических расчетах обычно считают, что процесс разбега заканчивается при скорости, равной не 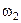, а 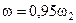, тогда время процесса получается конечное.

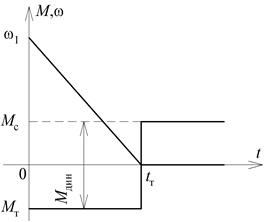
В тех случаях, когда динамический момент имеет отрицательное значение, привод замедляется (рис. 2.11). Для этого случая уравнение движения будет иметь вид:

.

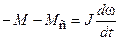Привод будет замедляться и в том случае, когда двигатель будет развивать момент, меньший статического, по абсолютному значению.

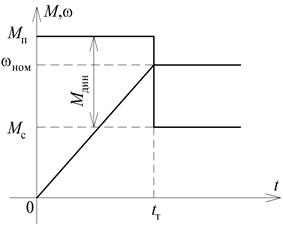
Рис. 2.10. Пусковой график привода	Рис. 2.11. Тормозной график привода

Время торможения привода

.

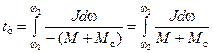Для частного случая, при ,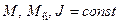

.

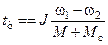Можно также посчитать оптимальное значение передаточного числа ПМ 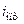при заданных значениях моментов инерции двигателя и механизма 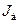и 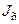, а также момента сопротивления .

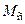Уравнение движения привода относительно рабочего вала механизма

,

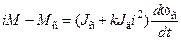где 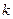– коэффициент, учитывающий момент инерции передач.

Очевидно, что минимальное время будет при максимальном ускорении привода

.

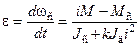Для нахождения оптимального передаточного числа найдем точку максимума функции .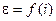

, .

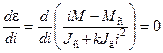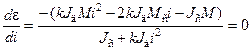Решая уравнение

,

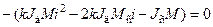получаем передаточное число ПМ

.

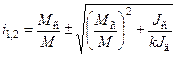Второе решение уравнения (со знаком минус перед вторым слагаемым) дает при всех соотношениях i отрицательные значения.