Энергетические зоны в модели Кронига-Пенни

Найдем в явном виде дисперсионное соотношение для электрона в периодическом кристаллическом поле. Исследуя выражение (2.14) находим, что волновое число k может быть вещественным только при условии, что значения левой части этого равенства находятся в интервале от -1 до +1. Зависимость левой части уравнения (2.14) от 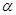для параметра p = 2 приведен на рис. 2.5. Заштрихованные участки соответствуют запрещенным значениям параметра 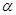и, следовательно, энергии электрона в кристалле. Этот результат получен только на основании теоремы Блоха, условием применимости которой является единственное требование периодичности потенциала в стационарном уравнении Шредингера для электрона в кристалле. Таким образом, наличие периодического потенциала приводит к появлению для энергии электрона таких интервалов, для которых нет волнового решения, соответствующего вещественным значениям волнового числа электрона. Результатом этого является чередование разрешенных и запрещенных зон энергии для электрона в кристалле.

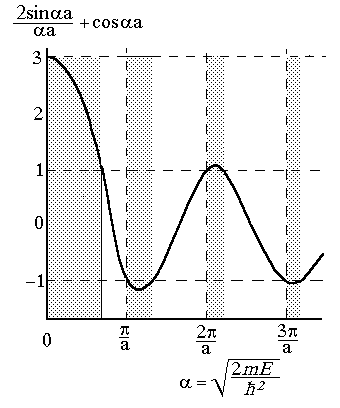
Рис. 2.5. Зависимость от параметра 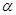левой части уравнения (2.14)

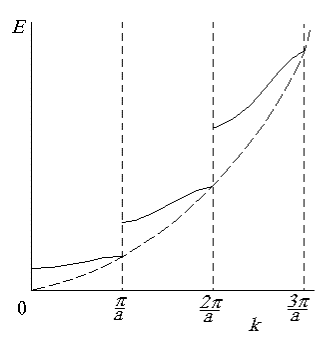
Рис. 2.6. Зависимость энергии электрона от волнового числа для p=2 и p=0 (штриховая линия)

На рис. 2.6 приведено дисперсионное соотношение для энергии электрона в кристалле. Видно, что зависимость E(k) претерпевает разрывы в точках, где 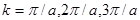и т. д.

Если параметр p = 0, согласно равенству (2.14) и

Последнее равенство соответствует дисперсионному соотношению для свободного электрона. На рис. 2.6 это дисперсионное соотношение изображено штриховой линией.

Поскольку, как подчеркивалось выше, все физически различимые значения волнового числа лежат в пределах первой зоны Бриллюэна, которая в одномерном случае ограничена интервалом значений волнового числа от - 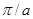до + 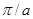, целесообразно перейти от представления расширенных зон Бриллюэна (рис. 2.6) к представлению приведенных зон Бриллюэна (рис. 2.7). Волновые функции, соответствующие вещественным k, могут быть построены только для заштрихованных областей энергии электрона. Эти области представляют собой разрешенные энергетические зоны, которые отделены друг от друга зонами (щелями) запрещенных энергий.

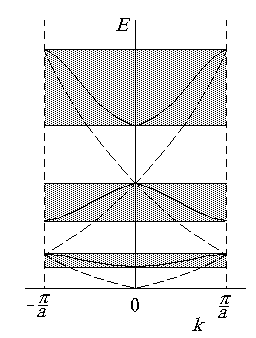
Рис.2.7. Энергия электрона как функция волнового числа в схеме приведенных зон Бриллюэна

Предел 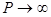дает дискретный ряд уровней

которые совпадают с полученными в первой главе результатами для частицы в одномерной прямоугольной потенциальной яме (см. уравнение (1.34)).Энергия электронов в периодическом поле кристалла претерпевает разрыв на границах зон Бриллюэна, для которых 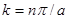. Физическая природа разрывов связана с отражением электронных волн от атомных плоскостей кристаллической решетки. Действительно, с учетом того, что 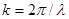, условие, при котором происходит нарушение непрерывности функции E(k), может быть записано в виде 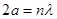, что совпадает с условием Вульфа-Брэгга при угле падения волн 90⁰.