Модель Кронига-Пенни
Теорема Блоха позволяет аналитически решить задачу об электроне в периодическом поле кристаллической решетки в приближении слабой связи при некоторых упрощающих предположениях. Основная трудность в решении уравнения (2.1) связана с невозможностью точно записать вид функции U(r). Поэтому часто периодическую зависимость функции U(r) заменяют более простой функцией с точно таким же периодом. В модели Кронига-Пенни ограничиваются рассмотрением одномерной задачи, в которой периодический потенциал заменяется цепочкой прямоугольных потенциальных ям (рис. 2.4). Ширина каждой ямы а, они отделены друг от друга прямоугольными потенциальными барьерами высотой U0 и шириной b. Период повторения ям с = а + b.
Стационарное уравнение Шредингера будет иметь в этом случае вид
 (2.7)
(2.7)
Начало системы координат (точку х = 0) выберем так, чтобы она совпадала с левым краем потенциальной ямы, как это показано на рис. 2.4,б. Tогда потенциальная функция
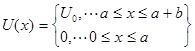 , (2.8)
, (2.8)
В соответствии с теоремой Блоха волновая функция электрона 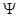 (x) может быть представлена в виде
(x) может быть представлена в виде
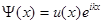 . (2.9)
. (2.9)

Рис.2.4. Изменение потенциальной энергии электрона: а - в реальном кристалле; б - в модели Кронига-Пенни
Индексы n и k упущены для простоты записи. Функция u(x) (блоховский множитель) имеет период c
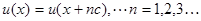
Подставляя (2.9) в уравнение (2.7), получим дифференциальное уравнение для блоховского множителя
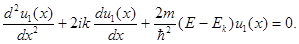 (2.10 a)
(2.10 a)
для электронов, находящихся внутри потенциальных ям, и
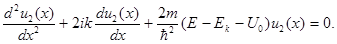 (2.10 б)
(2.10 б)
для электронов, находящихся вне потенциальных ям. В этих уравнениях Ek - кинетическая энергия электрона
 .
.
Общее решение уравнения (2.10 а) для электронов внутри потенциальных ям может быть записано в виде
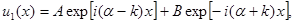 (2.11 а)
(2.11 а)
где 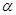 - некоторый параметр, который может быть найден подстановкой решения в виде (2.11 а) в исходное уравнение (2.10 а). Эта подстановка приводит к следующему значению
- некоторый параметр, который может быть найден подстановкой решения в виде (2.11 а) в исходное уравнение (2.10 а). Эта подстановка приводит к следующему значению 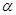 :
:

В области вне потенциальных ям при условии, что высота потенциального барьера U0 выше полной энергии электрона Е, решение уравнения (2.10 б) имеет вид
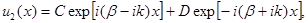 (2.11 б)
(2.11 б)
где
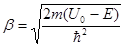 .
.
Постоянные A, B, C и D в формулах (2.11 а) и (2.11 б) находятся как обычно из граничных условий. Граничные условия требуют, чтобы функция u(x) и ее первая производная в местах скачков потенциала, т. е. на стенках потенциальных ям, были непрерывны. Эти требования приводят к следующей системе уравнений:
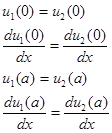 . (2.12)
. (2.12)
Система уравнений (2.12) после подстановки в нее функций  и
и  , согласно равенствам (2.10 а) и (2.10 б), преобразуется в систему линейных однородных алгебраических уравнений, в которых неизвестными являются коэффициенты A, B, C и D. Определитель этой системы будет равен нулю (только при этом условии система линейных однородных уравнений имеет отличные от нуля решения), если выполняется следующее равенство:
, согласно равенствам (2.10 а) и (2.10 б), преобразуется в систему линейных однородных алгебраических уравнений, в которых неизвестными являются коэффициенты A, B, C и D. Определитель этой системы будет равен нулю (только при этом условии система линейных однородных уравнений имеет отличные от нуля решения), если выполняется следующее равенство:
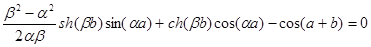 . (2.13)
. (2.13)
Выражение (2.13) можно значительно упростить, если допустить, что ширина барьера стремится к нулю  , а его высота - к бесконечности
, а его высота - к бесконечности 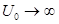 , но таким образом, чтобы произведение
, но таким образом, чтобы произведение 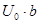 оставалось постоянным
оставалось постоянным 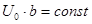 .
.  При этих условиях выражение (2.13) преобразуется к виду:
При этих условиях выражение (2.13) преобразуется к виду:
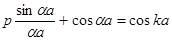 , (2.14)
, (2.14)
где 
Поскольку 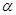 - параметр, определяемый энергией Е электрона, а k - волновой вектор электрона, то выражение (2.14) представляет зависимость E(k), т. е. дисперсионное соотношение для электрона в кристаллической решетке. Это дисперсионное соотношение можно записать в явном виде, решив уравнение (2.14) относительно
- параметр, определяемый энергией Е электрона, а k - волновой вектор электрона, то выражение (2.14) представляет зависимость E(k), т. е. дисперсионное соотношение для электрона в кристаллической решетке. Это дисперсионное соотношение можно записать в явном виде, решив уравнение (2.14) относительно 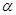 при фиксированном значении параметра p.
при фиксированном значении параметра p.
Дата добавления: 2021-10-28; просмотров: 479;











