Критерий идеального наблюдения (Котельникова)
Рассмотрим широко распространенный критерий Котельникова (идеального наблюдателя).
Будем называть критерием Котельникова такой критерий, согласно которому качество приемников (демодуляторов) оценивают величиной вероятности правильного приема символа (элемента сигнала).
Задание критерия необходимо для синтеза оптимального приемника.
Под синтезом будем понимать нахождение оптимальной в соответствии с некоторым критерием качества приема процедуры обработки наблюдаемого случайного процесса 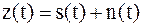 . Далее на этой основе создается устройство, которое реализует найденную процедуру обработки.
. Далее на этой основе создается устройство, которое реализует найденную процедуру обработки.
Итак, пусть на вход приемника (демодулятора) поступает аддитивная смесь сигнала и помехи: 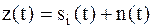 , на основе которой выносится решение о передаче символа
, на основе которой выносится решение о передаче символа 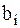 . Это происходит после вычисления апостериорной вероятности
. Это происходит после вычисления апостериорной вероятности 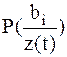 , т.е. вероятности того, что действительно передавался символ
, т.е. вероятности того, что действительно передавался символ 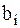 при поступлении на вход приемника
при поступлении на вход приемника 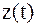 .
.
В этом случае критерию идеального наблюдателя будет соответствовать схема приемника (решающая схема), которая построена по правилу максимума апостериорной вероятности: регистрируется символ 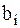 , если выполняется неравенство:
, если выполняется неравенство:
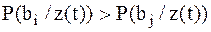 ; ;
| (2.1) |
Данное выражение сокращенно можно записать:
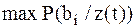 ; ;
| (2.2) |
При передаче двоичных сигналов данное правило принимает вид:
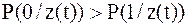 ; ;
|
Если неравенство выполняется, то регистрируется символ «1», в противном случае – «0».
Воспользуемся формулой Байеса:
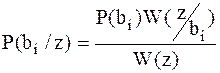 ; ;
| (2.3) | |||
| где | 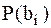
| – | априорная вероятность передачи символа 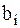 (определяется до момента наблюдения и начала анализа сигнала) (определяется до момента наблюдения и начала анализа сигнала)
| |
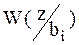
| – | условная плотность вероятности, определяемая выбором решающей схемы и свойством помех в канале – условная плотность распределения колебания 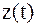 при передаче символа при передаче символа 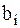 . Иначе – функция правдоподобия. . Иначе – функция правдоподобия.
| ||
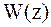
| – | безусловная плотность вероятности 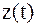 не являющаяся функцией не являющаяся функцией 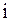
| ||
Учитывая, что 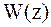 не зависит от
не зависит от 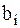 , получим:
, получим:
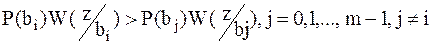
| (2.4) |
Приемник, реализующий правило (2.4), получил название критерия идеального наблюдателя (приемника Котельникова). При передаче двоичных символов данное соотношение принимает вид:
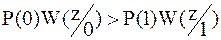 ; ;
|
Если неравенство выполняется, то регистрируется символ 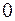 , в противном случае –
, в противном случае – 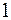 .
.
Выражение (2.4) можно представить в виде отношения функций правдоподобиядвух гипотез о передаче символов 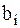 и
и 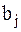 .
.
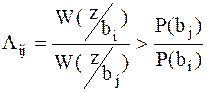 ; ;
| (2.5) |
В случае, когда все сообщения передаются равновероятно, т.е. 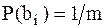 , то данное правило упрощается:
, то данное правило упрощается:
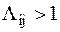 , ,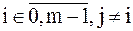
| (2.6) |
В реальных системах (передачи дискретной информации) связи данная ситуация наблюдается довольно часто – все символы от источника передаются как правило с одинаковыми вероятностями.
Итак, правило (2.6), реализующее критерий идеального наблюдателя при равновероятных символах сообщения, называютправилом (критерием) максимального правдоподобия.
Его достоинство – отсутствие априорных сведений о передаваемых символах 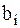 .
.
Недостаток – равная вероятность появления любой из ошибок ( 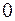 или
или 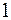 ).
).
Рассмотрим бинарную систему, в которой передача сообщений осуществляется с помощью двух сигналов 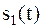 и
и 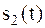 , соответствующих двум кодовым символам
, соответствующих двум кодовым символам 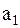 и
и 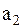 . Решение принимается по результату обработки принятого колебания
. Решение принимается по результату обработки принятого колебания 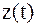 пороговым методом: регистрируется
пороговым методом: регистрируется 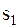 , если
, если 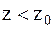 , и
, и 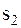 , если
, если 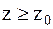 , где
, где 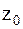 – некоторый пороговый уровень. Здесь могут возникнуть ошибки двух видов: воспроизводится s1, когда передавался
– некоторый пороговый уровень. Здесь могут возникнуть ошибки двух видов: воспроизводится s1, когда передавался 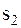 и
и 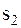 , когда передавался
, когда передавался 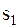 . Условные вероятности этих ошибок (вероятности переходов) будут равны:
. Условные вероятности этих ошибок (вероятности переходов) будут равны:
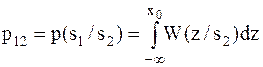 – условная вероятность передачи
– условная вероятность передачи 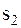 при условии приема
при условии приема 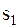
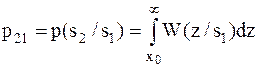 – условная вероятность передачи
– условная вероятность передачи 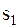 при условии приема
при условии приема 
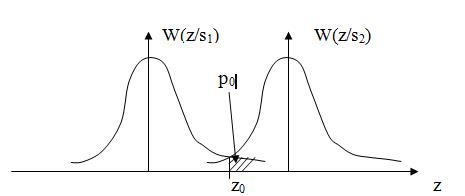
Значения этих интегралов могут быть вычислены как соответствующие площади, ограниченные графиком плотностей условного распределения вероятностей (рис. 2)
|
Рис. 2. График плотности условного распределения вероятностей при передаче сигналов 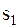 и и 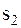 . .
|
Вероятности ошибок первого и второго вида соответственно:
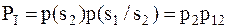 ,
,
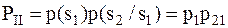 .
.
При этом полная вероятность ошибки равна:
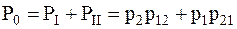 .
.
Пусть 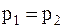 , тогда
, тогда
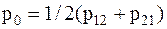 .
.
В этом случае минимум 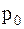 имеет место при
имеет место при 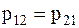 ., т. е. при выборе порога в соответствии с рис. 2.
., т. е. при выборе порога в соответствии с рис. 2.
Выводы
1. В системах связи в качестве критерия оптимального приема сообщений (критерий идеального наблюдателя) используют критерий максимума апостериорной вероятности (вероятности правильного приема символа).
2. При равновероятной передаче различных символов критерий идеального наблюдателя реализуется правилом максимального правдоподобия.
Дата добавления: 2017-11-21; просмотров: 5570;











