ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СМО

Рассмотрим параметры и характеристики, которые являются общими для всех видов СМО.

Первичные свойства СМО, как правило, не зависящие от разработчика СМО и являющиеся исходным материалом для дальнейших расчетов, называются параметрами.

Параметры СМО.

1. Интенсивность входного потока заявок - l.

2. Интенсивность потоков ухода заявок из очереди и обслуживающего прибора без обслуживания - _.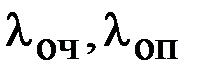

3. Трудоемкость прикладных программ - q.

Вторичные свойства СМО зависят от требований разработчика и называются характеристиками.

Характеристики СМО.

1. Приведенная интенсивность входящего потока заявок, равна среднему количеству заявок, поступивших в СМО за время обслуживания в обслуживающем приборе одной заявки.

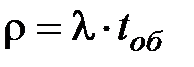, (3.3)

где t_об - время обслуживания в ОП одной заявки.

Так как

,

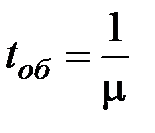то

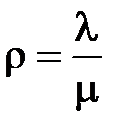. (3.4)

При r<1 в СМО поддерживается стационарный режим работы, при котором очередь со временем не возрастает. При r>1 в СМО устанавливается нестационарный режим, в результате чего начинает возрастать очередь, что ведет к перегрузке СМО.

Если СМО имеет несколько ОП и все ОП идентичны по своим характеристикам, а потоки заявок простейшие, то можно считать, что с вероятностью 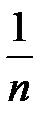любая заявка попадет на один из ОП. Тогда

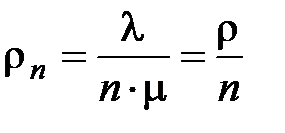. (3.5)

2. Приведенная интенсивность потока заявок, покидающих СМО без обслуживания.

Среднее количество заявок, покидающее СМО из очереди

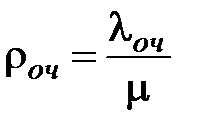
и из обслуживающего прибора

.

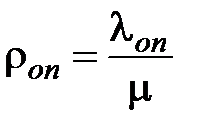Последними двумя формулами выражается среднее количество заявок, покидающее СМО за время обслуживания в ОП одной заявки.

3. Количество потоков заявок (N). Заявки могут объединяться в потоки по следующим признакам:

- интенсивности поступления в СМО;

- приоритету обслуживания обслуживающим прибором;

- принадлежности к виду технологического оборудования;

- длительности прикладных программ.

На вход СМО могут поступать несколько простейших потоков заявок с одинаковыми приоритетами и трудоемкостями прикладных программ. Все эти потоки заявок возможно объединить в один суммарный поток. При сложении нескольких независимых, ординарных, стационарных случайных потоков заявок образуется суммарный поток заявок, приближающийся по своим свойствам к простейшему.

Если входной поток заявок представляет собой сумму N простейших потоков заявок с интенсивностями 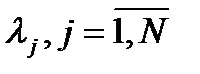, то его можно характеризовать суммарной интенсивностью и суммарной приведенной интенсивностью

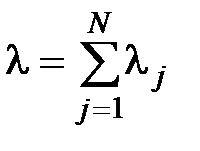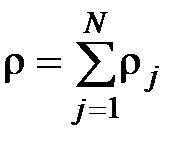, . (3.6)

При суммировании нескольких простейших потоков заявок с различными уровнями приоритетов суммарная приведенная интенсивность выразится как

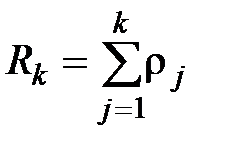, (3.7)

где k - количество суммируемых потоков заявок.

4. Количество заявок, находящихся в данный момент в очереди,

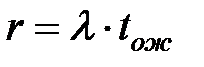, (3.8)

где t_ож - время ожидания одной заявки в очереди.

При r>1 оценка количества заявок в очереди может производится по формуле

,

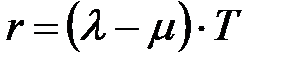где Т - время, в продолжение которого оценивается количество заявок в очереди.

5. Количество заявок, находящихся одновременно в СМО в данный момент времени,

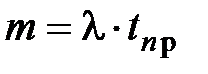, (3.9)

где t_пр - время пребывания одной заявки в СМО.

В общем случае

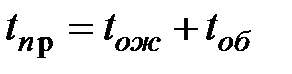. (3.10)

Если в выражении (3.10) левую и правую части умножить на l

,

то можно записать

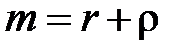. (3.10)

6. Количество мест в очереди (d). В общем случае d¹r.

Обозначение СМО состоит из 4 полей. Поля разделяются наклонными прямыми линиями. В первом и втором полях указываются законы распределения вероятностей потоков заявок и дисциплин обслуживания соответственно.

M - простейший закон распределения вероятности.

Е - поток Эрланга.

D - детерминированный поток.

G - прочие потоки.

В третьем поле указывается количество обслуживающих приборов.

В четвертом поле указывается количество мест в очереди.

Например,

M/M/n=1/d=5.

В рассматриваемой СМО поток заявок и дисциплина обслуживания подчинены простейшему закону распределения вероятностей. В СМО имеется один обслуживающий прибор и пять мест в очереди.

3.2.5. Одноканальные СМО с ограниченным количеством мест в
очереди и терпеливыми заявками

Рассмотрим СМО с ограниченным количеством мест в очереди, с одним обслуживающим прибором (одноканальная СМО, n=1) и в предположении, что все заявки, поступающие на вход СМО, являются терпеливыми. В этом случае можно считать, что 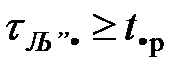. Иначе это можно записать как

.

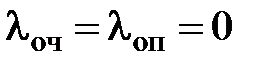В то же время при полностью заполненной очереди поступившая заявка на обслуживание не принимается СМО и теряется.

Формула для нахождения вероятности простоя СМО

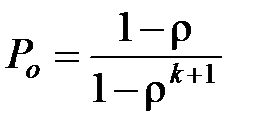. (3.12)

Формула для вероятности нахождения СМО в одном из i-х состояний

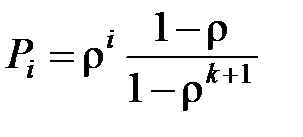. (3.13)

При k=j=n+d (при полностью заполненных местах в обслуживающем приборе и очереди) вероятность состояния СМО будет равна

.

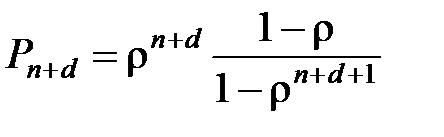Эта вероятность состояния СМО называется вероятностью отказа и обозначается как P_отк.

Если учесть, что рассматривается одноканальная СМО (n=1), то выражения (3.12) и (3.13) для определения вероятностей простоя СМО и отказа обслуживания заявки можно записать в виде

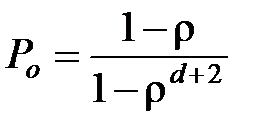, (3.14)

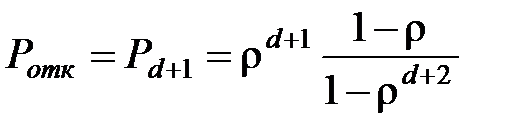. (3.15)

Вероятность обслуживания заявки в СМО будет равна

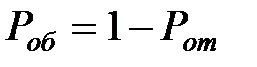. (3.16)

Зная количество заявок, находящихся в СМО в данный момент времени при данном ее состоянии, и зная вероятность каждого состояния СМО, возможно определить среднее количество заявок, которое может находиться в СМО при данном количестве обслуживающих приборов, данном количестве мест в очереди и заданной интенсивности входного потока заявок. Для нахождения среднего количества заявок используется выражение для определения математического ожидания вида

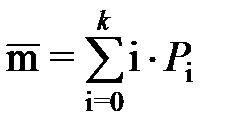,(3.17)

где i - номер состояния СМО;

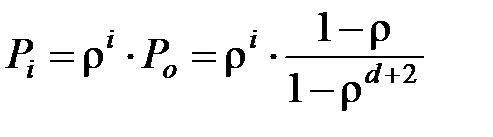
- вероятность нахождения СМО в одном из i-х состояний.

Для одноканальной СМО n=1.Поэтому выражение для среднего значения количества заявок в СМО примет вид

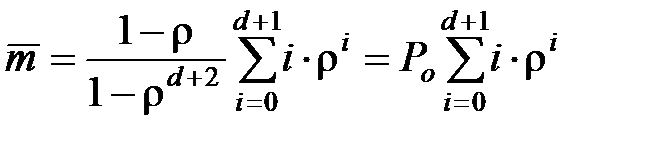. (3.18)

Формулы (3.14), (3.15) и (3.18) могут быть использованы только для расчета характеристик одноканальных СМО с ограниченным количеством мест в очереди и терпеливыми заявками.

3.2.6. Многоканальные СМО с ограниченным количеством мест
в очереди и с нетерпеливыми заявками

Рассмотрим СМО с несколькими обслуживающими приборами (n>1), с ограниченным количеством мест в очереди и возможными потерями заявок в очереди (l_оч¹0) и в обслуживающем приборе (l_оп¹0) за счет нетерпеливости заявок. При задержке заявки в СМО больше допустимого времени 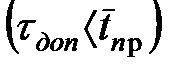информация заявки устаревает, и она вынуждена покинуть СМО из того устройства, в котором она находилась в данный момент (очереди или обслуживающем приборе). При полностью заполненной очереди вновь поступившая заявка получает отказ в обслуживании и теряется.

Используя формулы Эрланга, возможно получить выражения для предельных значений вероятностей состояний СМО при заполнении заявками обслуживающего прибора, но при пустой очереди,

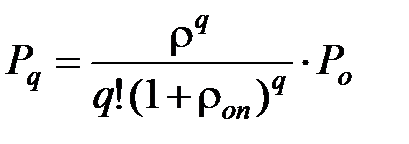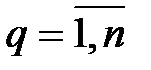при (3.19)

и при заполнении мест в очереди, но при полностью заполненном обслуживающем приборе,

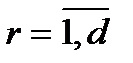при и 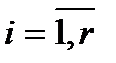. (3.20)

При r=d и q=n рассчитывается вероятность отказа заявке в обслуживании.

Вероятность простоя СМО (Р_о) определяется из условия равенства единице суммы вероятностей всех состояний СМО

Подставив в эту формулу выражения для Р_q (3.19) и Р_n+d (3.20) получим окончательно

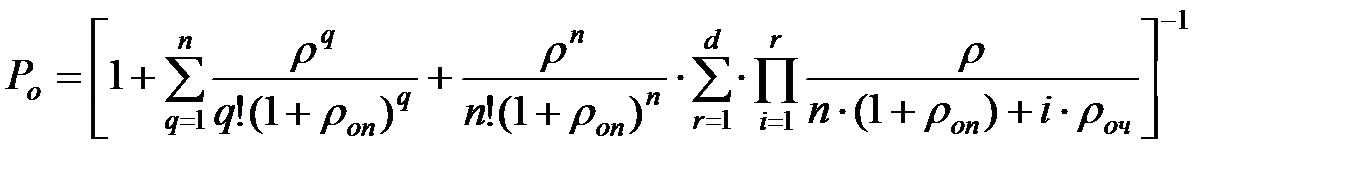. (3.21)

Среднее количество заявок в очереди равно трем.

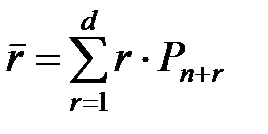. (3.22)

Вопросы для самопроверки по теме 3.2

1. Какие технические задачи решаются при помощи теории массового обслуживания?
2. По каким признакам классифицируются системы массового обслуживания?
3. Какие параметры системы массового обслуживания характеризуют функция распределения и плотность распределения?
4. Что характеризуют собой вероятности состояний СМО?
5. Почему при расчете вероятностей состояний СМО с ограниченным количеством мест в очереди и с нетерпеливыми заявками используются две формулы: при заполнении ОП и при заполнении очереди?