Превращение энергии при колебательном движении
Вычислим энергию тела массой m, совершающего свободные гармонические колебания с амплитудой x0, и циклической частотой w0. Потенциальная энергия Еп тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила 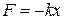 (для пружинного маятника; для других систем аналогично), перемещая тело в положение равновесия. Эту работу можно найти, воспользовавшись формулой
(для пружинного маятника; для других систем аналогично), перемещая тело в положение равновесия. Эту работу можно найти, воспользовавшись формулой
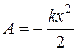 ,
,
откуда
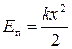 .
.
Заменив х по формуле 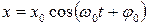 , получим
, получим
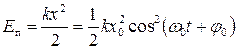 .
.
Кинетическую энергию найдем, подставив в формулу 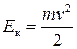 выражение для
выражение для 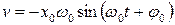 :
:
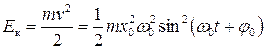 .
.
Заменив в уравнении для потенциальной энергии k через 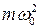 и сложив почленно выражения для
и сложив почленно выражения для 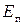 и
и 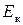 , получим следующее выражение для полной энергии Е колеблющегося тела:
, получим следующее выражение для полной энергии Е колеблющегося тела:
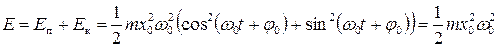 .
.
Таким образом, полная механическая энергия тела, совершающего гармонические колебания, пропорциональна квадрату амплитуды колебаний. В случае свободных незатухающих колебаний полная механическая энергия не должна зависеть от времени. Поэтому амплитуда x0 колебаний тоже не зависит от времени.
Потенциальная и кинетическая энергия колеблющегося тела пропорциональны квадрату амплитуды колебаний. Кинетическая и потенциальная энергии при свободных незатухающих гармонических колебаниях изменяются периодически.
Однако период изменения энергии в два раза меньше периода изменения смещения, скорости и ускорения. За время одного полного колебания кинетическая и потенциальная энергии дважды достигают своих амплитудных значений и дважды обращаются в нуль. Это связано с тем, что 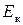 и
и 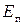 пропорциональны квадратам косинуса и синуса фазы колебаний.
пропорциональны квадратам косинуса и синуса фазы колебаний.
Максимальная потенциальная энергия тела, совершающего свободные гармонические колебания равна 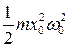 . Максимальная кинетическая энергия этого тела также равна
. Максимальная кинетическая энергия этого тела также равна 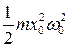 .
.
Дата добавления: 2021-09-25; просмотров: 563;











