Свободные затухающие колебания

На практике всякое колебание, которое не поддерживается извне, затухает, амплитуда его колебания с течением времени уменьшается. Причина затухания обуславливается силами, тормозящими движение, например, силой трения в месте подвеса при колебании маятника или силой сопротивления среды. Чтобы исследовать этот вопрос, надо написать уравнение, выражающее второй закон Ньютона, принимая в расчет силы сопротивления. Мы ограничимся рассмотрением случая, когда точка совершает прямолинейное колебание в вязкой среде. Сила сопротивления среды зависит от скорости движения точки и в случае малых скоростей ее можно считать пропорциональной скорости v; направлена она в сторону, противоположную скорости; таким образом, силу сопротивления можно положить равной , где r – постоянная величина, называемая коэффициентом сопротивления. 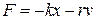Эта сила прибавится к упругой силе –kx, откуда полная сила, действующая на точку, равна и, следовательно, второй закон Ньютона может быть написан в виде:

.

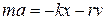Решение последнего уравнения имеет вид

,

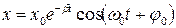где введены обозначения 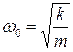и .

Это решение представляет собою колебание с амплитудой , уменьшающейся с течением времени. Период колебания в среде с сопротивлением больше, чем период колебания 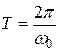такой же массы m под действием такой же упругой силы 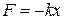в среде без сопротивления. График зависимости х от времени представлен на рисунке. Как видно, колебания затухают со временем.

Логарифм отношения двух последовательных значений амплитуд, отстоящих друг от друга на время, равное периоду Т, называется логарифмическим декрементом затухания

.

Поясним физический смысл величин l и b. Обозначим через t промежуток времени, за который амплитуда колебаний уменьшается в e paз. Тогда

,

откуда , или

.

Следовательно, коэффициент затухания b есть физическая величина, обратная промежутку времени t, в течение которого амплитуда убывает в е раз. Величину t называют временем релаксации. Пусть, например, b= 10²с^-1 – это означает, что амплитуда колебаний убывает в е раз за 10^-2 с. Пусть N – число колебаний, после которых амплитуда уменьшается в е раз. Тогда

,

.

Следовательно, логарифмический декремент затухания l есть физическая величина, обратная числу колебаний N, по истечении которых амплитуда убывает в е раз. Пусть, например, l = 0,01. Это значит, что амплитуда колебаний убывает в е раз по истечении 100 колебаний.