Энергия магнитного поля

Рассмотрим цепь, изображенную на рисунке. Сначала замкнем соленоид L на батарею E ; в нем установится ток I, который обусловит магнитное поле, сцепленное с витками соленоида. Если, отключив соленоид от батареи, замкнуть его через сопротивление R, то в образовавшейся цепи будет некоторое время течь постепенно убывающий ток, подчиняющийся закону Ома для полной цепи

I = E_s /R

где E_s 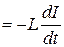– ЭДС самоиндукции (предполагаем, что проводники с током находятся в неферромагнитной однородной и изотропной среде, сопротивлением соленоида пренебрегаем).

Таким образом

E_s = IR.

Умножим обе части данного выражения на IDt:

E_s IDt = I²RDt.

Правая часть равенства представляет собой количество теплоты, выделяемое в проводнике при протекании в нем тока.

Левая часть данного равенства представляет собой элементарную работу, совершаемую током за время Dt, обусловленную индукционными явлениями. Полная работа, совершаемая в цепи за все время, в течение которого происходит исчезновение магнитного поля, равная сумме элементарных работ, есть:

.

Данная работа идет на приращение внутренней энергии проводников, т. е. на их нагревание. Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток I, обладает энергией

,

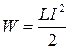которая локализована в возбуждаемом током магнитном поле.

Выразим энергию магнитного поля через величины, характеризующие само поле. В случае бесконечного соленоида

, ,

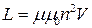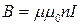откуда

.

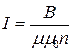Подставляя эти значения L и I в выражение для энергии и производя преобразования, получим

.

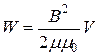Магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия заключена в пределах соленоида и распределена по его объему с постоянной плотностью w, которую можно получить, разделив W на V. Произведя это деление, получим

.

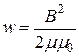Полученное выражение для плотности энергии магнитного поля имеет вид, аналогичный выражению для плотности энергии электрического поля, с тем лишь отличием, что электрические величины в нем заменены соответствующими магнитными.

Вопросы для самоконтроля:

1. В чем состоит явление электромагнитной индукции? Опишите опыты Фарадея.

2. Что называется магнитным потоком?

3. Сформулируйте закон Фарадея и правило Ленца для электромагнитной индукции. Проиллюстрируйте их примерами.

4. Как определяется направление индукционного тока?

5. Сформулируйте основной закон электромагнитной индукции.

6. В чем состоит явление самоиндукции?

7. Что называется индуктивностью проводящего контура?

8. От чего зависят индуктивность проводящего контура и каков ее физический смысл?

9. Напишите выражение для ЭДС самоиндукции.

10. В чем состоит явление взаимной индукции?

12. Напишите выражения для ЭДС взаимной индукции.

13. Что называется взаимной индуктивностью двух контуров? От чего она зависит и каков ее физический смысл?

14. Приведите выражение для объемной плотности энергии магнитного поля.

15. Как распределена энергия магнитного поля соленоида в пространстве?