Круговые (циклические) процессы.
В термодинамике наряду с понятием равновесного состояния большую роль играет понятие обратимого процесса.
Обратимым процессом называется такой процесс, при котором возможен обратный переход системы из конечного состояния в начальное через те же промежуточные состояния, чтобы в окружающих телах не произошло никаких изменений. Обратимый процесс является физической абстракцией. Примером процесса, приближающегося к обратимому, является колебание тяжелого маятника на длинном подвесе. В этом случае кинетическая энергия практически полностью превращается в потенциальную, и наоборот. Колебания происходят долго без заметного уменьшения амплитуды ввиду малости сопротивления среды и сил трения.
Обратимым может быть только равновесный процесс.
Обратимый процесс, очевидно, обладает следующим свойством: если при прямом ходе на каком-то элементарном участке система получает тепло DQ1 и совершает работу DA1 , то при обратном ходе на том же участке система отдает тепло DQ2 = DQ1 и над ней совершается работа DA2 = DA1. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращения системы в первоначальное состояние в окружающих систему телах не должно оставаться никаких изменений.
Любой процесс, сопровождаемый трением или теплопередачей от нагретого тела к холодному, называется необратимым процессом. Примером необратимого процесса является расширение газа, даже идеального, в пустоту. Расширяясь, газ не преодолевает сопротивления среды, не совершает работы, но для того чтобы вновь собрать все молекулы газа в прежний объем, т. е. привести газ в начальное состояние, необходимо затратить работу. Таким образом, все реальные процессы являются необратимыми.
Круговым процессом (или циклом) называется такой процесс, при котором система после ряда изменений возвращается в исходное состояние. На графике цикл изображается замкнутой кривой (см. рис.). Работа, совершаемая при круговом процессе, численно равна площади, охватываемой кривой. В самом деле, работа на участке 1–2 положительна и численно равна площади, отмеченной наклоненной вправо штриховкой (рассматривается цикл, совершаемый по часовой стрелке). Работа на участке 2–1 отрицательна и численно равна площади, отмеченной наклоненной влево штриховкой. Следовательно, работа за цикл численно равна площади, охватываемой кривой, и будет положительна при прямом цикле (т. е. таком, который совершается в направлении по часовой стрелке) и отрицательна при обратном.
 После совершения цикла система возвращается в прежнее состояние. Поэтому всякая функция состояния, в частности внутренняя энергия, имеет в начале и в конце цикла одинаковое значение.
После совершения цикла система возвращается в прежнее состояние. Поэтому всякая функция состояния, в частности внутренняя энергия, имеет в начале и в конце цикла одинаковое значение.
 Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объема V2, а затем снова сжимается до первоначального объема V1. Чтобы работа за цикл была больше нуля, давление (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать тепло, а в ходе сжатия отнимать от него тепло.
Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объема V2, а затем снова сжимается до первоначального объема V1. Чтобы работа за цикл была больше нуля, давление (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать тепло, а в ходе сжатия отнимать от него тепло.
Напишем уравнение первого начала термодинамики для обеих частей цикла. При расширении внутренняя энергия изменяется от значения U1 до U2, причем система получает тепло Q1 и совершает работу А1. Согласно первому началу
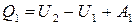 .
.
При сжатии система совершает работу А2 и отдает тепло Q2. что равнозначно получению тепла –Q2. Следовательно,
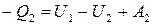 .
.
Складывая последние два уравнения, получаем:
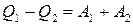 .
.
Замечая, что А1 + А2 есть полная работа А, совершаемая системой за цикл, можно написать:
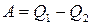 .
.
Периодически действующий двигатель, совершающий работу за счет получаемого извне тепла, называется тепловой машиной.
Из последней формулы следует, что не все получаемое извне тепло Q1 используется для получения полезной работы. Для того чтобы двигатель работал циклами, часть тепла, равная Q2, должна быть возвращена во внешнюю среду и, следовательно, не используется по назначению (т. е. для совершения полезной работы). Очевидно, что чем полнее превращает тепловая машина получаемое извне тепло Q1 в полезную работу А, тем эта машина выгоднее. Поэтому тепловую машину принято характеризовать коэффициентом полезного действия h (сокращенно КПД), который определяется как отношение совершаемой за цикл работы А к получаемому за цикл теплу Q1:
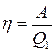 .
.
 Поскольку согласно
Поскольку согласно 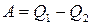 , выражение для КПД можно записать в виде
, выражение для КПД можно записать в виде
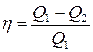 .
.
Цикл Карно.
Наиболее простым по содержанию, но важным в принципиальном отношении, является цикл Карно. Он состоит из двух изотерм при температурах Т1 и Т2 между состояниями 1, 2 и 3, 4 и двух адиабат между состояниями 2, 3 и 4, 1. Направление цикла указано стрелками. При выполнении цикла Карно необходимы два термостата. Термостат с более высокой температурой T1 называется нагревателем, а с более низкой температурой Т2 – холодильником. При прохождении адиабатических участков цикла система должна быть изолирована от окружающей среды в тепловом отношении, т. е. не должна обмениваться теплом с окружающей средой.
КПД цикла Карно равен
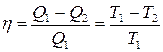 .
.
КПД определяется лишь температурами нагревателя и холодильника и не зависит от рода рабочего вещества.
Из последнего уравнения следуют выводы:
1. Для повышения КПД тепловой машины нужно увеличивать температуру нагревателя и уменьшать температуру холодильника.
2. КПД тепловой машины всегда меньше 1.
Дата добавления: 2021-09-25; просмотров: 770;











