Беспилотный летательный аппарат как объект управления.

Исследование автоматической системы выполним на примере системы стабилизации углового движения беспилотного летательного аппарата (БПЛА). Динамика углового движения БПЛА описывается векторным уравнением

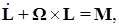
где 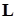– вектор момента количества движения; 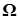– абсолютная угловая скорость относительно центра масс; 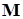– вектор действующих моментов.

Запишем векторное уравнение углового движения БПЛА в проекциях на оси связанной с летательным аппаратом системы координат

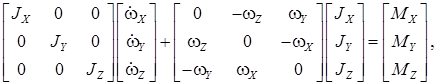
где 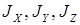– главные моменты инерции БПЛА относительно осей связанной системы координат 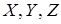; 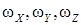– проекции вектора угловой скорости БПЛА на оси связанной системы координат; 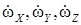– производные от проекций вектора угловой скорости на оси связанной системы координат; 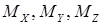– моменты, действующие на БПЛА относительно осей связанной системы координат.

Главные моменты инерции 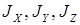зависят от распределения масс относительно осей БПЛА. Моменты 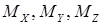определяются углами отклонения элеронов ( 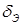), руля направления ( 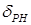) и руля высоты ( )

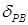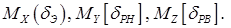
Интегрированием векторного уравнения углового движения БПЛА вычисляются проекции угловых скоростей относительно главных осей летательного аппарата. Углы ориентации БПЛА ( 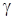– угол крена; 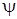– угол рысканья; 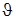– угол тангажа) вычисляются интегрированием системы дифференциальных уравнений

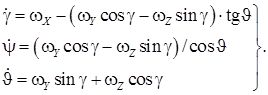
Применим к записанным выше системам уравнений преобразование Лапласа, выразим углы ориентации БПЛА относительно углов отклонения управляющих поверхностей ( 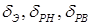), представим полученные зависимости в виде передаточных функций углового движения БПЛА: 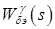– передаточная функция канала крена; 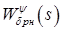– передаточная функция канала рысканья; 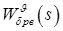– передаточная функция канала тангажа.