Передаточные функции различных систем.
Передаточные функции разомкнутой и замкнутой систем.
Рассмотрим структурную схему САУ, работающей по замкнутому циклу (см. рис.39)
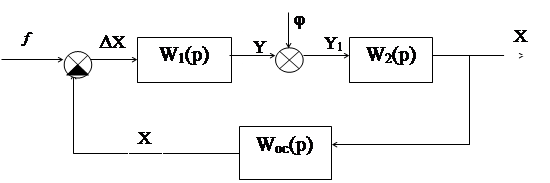 |
Рис.39
Здесь f – задающее воздействие
φ – возмущающее воздействие
x – управляемая переменная ( выходная величина САУ ).
Используя принцип суперпозиции, рассмотрим в отдельности передаточные функции по задающему и возмущающему воздействиям.
При определении передаточных функций по задающему воздействию будем полагать 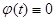 .Тогда с использованием правил структурных преобразований получим
.Тогда с использованием правил структурных преобразований получим
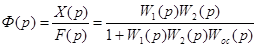 (25)
(25)
Передаточная функция замкнутой системы по ошибке
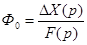
определяется из системы уравнений
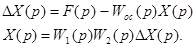
Исключая из последней системы X(p) , получим

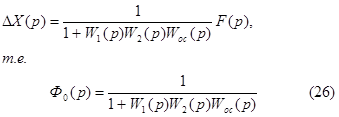
В выражениях (25), (26) участвует так называемая передаточная функция разомкнутой системы
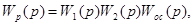
Которое определиться как отношение изображения X1(p) к изображению ∆X(p) при нулевых начальных условиях
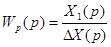 .
.
Передаточная функция разомкнутой системы имеет большое значение в теории автоматического регулирования . Многие методы анализа и синтеза САУ основаны на использовании этой функции.
Передаточная функция САУ по возмущающему воздействию определится выражением
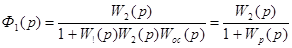 (27)
(27)
Рассмотрим замкнутую систему с единичной обратной связью при наличии только задающего воздействия . Структурная схема системы приведена на рис. .Она получается из предыдущей схемы при Woc(p)=1 и W(p)=W1(p)W2(P) .
 |
Рис.40
В этом случае зависимости (25), (26) принимают вид
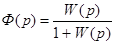 (28)
(28)
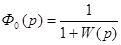 (29)
(29)
Здесь W(p) – передаточная функция разомкнутой системы .
Передаточная функция статической и астатической систем.
Рассмотрим замкнутую систему с единичной обратной связью . Пусть f(t)=1(t). Тогда F(p)=1/p и изображение сигнала ошибки ∆x(t) имеет вид
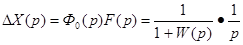 .
.
Обозначим 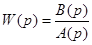 , где A(p) , B(p) – многочлены , не имеющие общих множителей ,
, где A(p) , B(p) – многочлены , не имеющие общих множителей ,
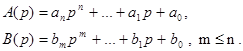
Тогда
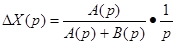
Найдем
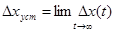
По теореме о предельном переходе
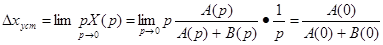 (30)
(30)
Из этого следует , что , так как A(0)+B(0) 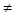 0 , то
0 , то
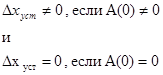
В первом случае мы имеем дело со статической системой и , таким образом , у нее передаточная функция разомкнутой системы имеет отличный от нуля свободный коэффициент характеристического многочлена , т.е.
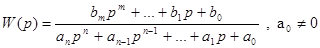
Общий случай.
Во втором случае система является астатической .При этом А(0)=0 , т.е. а0=0 и передаточная функция разомкнутой системы имеет вид

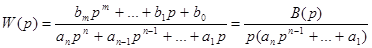 (31)
(31)
Система с такой передаточной функцией называется системой с астатизмом первого порядка.
В случае , когда а0=а1=0 имеем
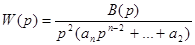 (32)
(32)
Это передаточная функция разомкнутой системы с астатизмом второго порядка. Очевидно , что при этом для входного сигнала f(t)=gt
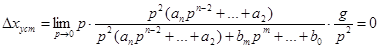
Рассмотрим общий случай . Пусть
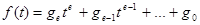 (33)
(33)
и
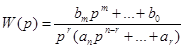
Тогда с использованием теоремы о предельном переходе получим
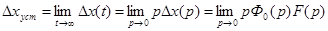 .
.
Из (33) имеем
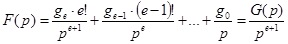 ,
,
где 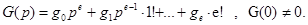
Выражение для Ф0(p) – передаточной функции замкнутой системы по ошибке имеет вид
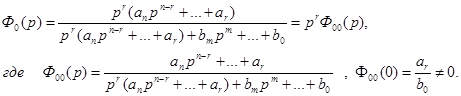
Тогда с учетом введенных обозначений
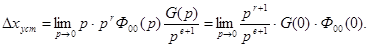
Могут представится три случая :
1. r > e , т.е. порядок астатизма больше степени номинального входного сигнала . При этом 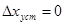
2. r = e . При этом
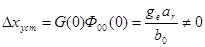
и является конечной величиной.
3. r < e , т.е. порядок астатизма меньше степени номинального входного сигнала. При этом 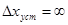 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Передаточная функция. Структурный анализ непрерывных линейных САУ. | | | Временные характеристики САУ. |
Дата добавления: 2017-10-04; просмотров: 3066;











