Передаточная функция. Структурный анализ непрерывных линейных САУ.
Передаточная функция.
До настоящего времени САУ описывались дифференциальным уравнением (18). Однако от этого уравнения можно перейти к другой характеристике – передаточной функции САУ, наиболее часто применяемой в инженерной практике.
Вернемся к дифференциальному уравнению (18)
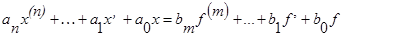
Перейдем от дифференциального уравнения к уравнению в изображениях при нулевых начальных условиях:

где D(p)= 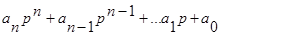
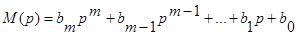
Из (21)
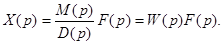
Передаточная функция САУ определяется как отношение преобразования Лапласа выходной величины системы к преобразованию Лапласа входной величины при нулевых начальных условиях

Передаточная функция представляет собой символическую запись дифференциального уравнения САУ. Она не зависит от входного сигнала и характеризует собственно систему (или ее часть если рассматривается передаточная функция одного или нескольких элементов САУ).
Для уравнения (18) передаточная функция W(p) имеет вид
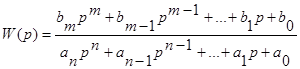 .
.
Для элементов, описываемых обыкновенными дифференциальными уравнениями с постоянными коэффициентами, передаточные функции являются дробно-рациональными функциями “p”. Многочлен, стоящий в знаменателе передаточной функции, называется характеристическим многочленом системы. Степень n характеристического многочлена называют порядком передаточной функции. (порядок системы). Физически реализуемые устройства имеют передаточную функцию, у которой степень числителя не превышает степень знаменателя. С помощью передаточных функций составляются структурные схемы САУ. В этих схемах показывают входные и выходные сигналы САУ и ее отдельных элементов и передаточные функции, связывающие изображения этих сигналов (см. рис. 30).
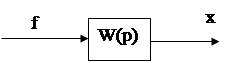 |
Рис.30
Пример. Пусть дифференциальное уравнение САУ имеет вид
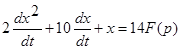
Переходим к уравнению в изображениях при нулевых начальных условиях:
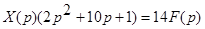
откуда 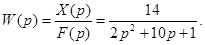
Необходимо также уметь перейти от передаточной функции к уравнению системы. Здесь можно выделить следующие этапы:
1.Записываем передаточную функцию в виде дробно-рационального выражения
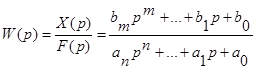 .
.
2.Переходим к уравнению в изображениях
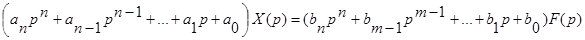
3.Переходим к дифференциальному уравнению относительно оригиналов, помня, что
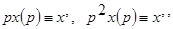
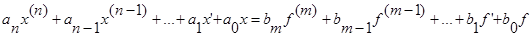
Пример. Пусть 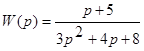 . Записать дифференциальное уравнение САУ.
. Записать дифференциальное уравнение САУ.
Решение. Имеем последовательно:
1. 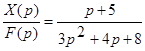
2. 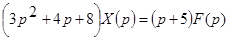
3. 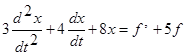
Структурный анализ непрерывных линейных САУ.
В ТАУ широко применяются структурные схемы. Структурная схема САУ представляет собой графическое изображение звеньев, входящих в систему, и связей между ними, соответствующих уравнению данной системы. В структурной схеме каждое звено задается своей передаточной функцией.
Элементы структурных схем: звенья изображаются прямоугольниками, со стоящими в них передаточными функциями; связи изображаются линиями со стрелками. Кроме того элементами схемы являются

Сумматор
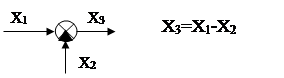
Элемент сравнения
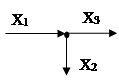
Узел (ответвление)
При анализе сложных схем САУ нужно уметь определять передаточные функции соединений элементов по передаточным функциям элементов, входящих в соединение. В практике наиболее часто встречаются три возможных типа соединения звеньев.
1.Последовательное соединение звеньев. При этом соединении выходной сигнал предыдущего элемента является входным сигналом последующего. Структурная схема последовательного соединения показана на рис.31.
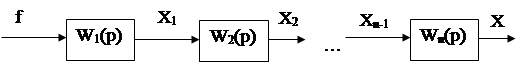 |
Рис.31
Определим передаточную функцию соединения, если известны передаточные функции отдельных звеньев
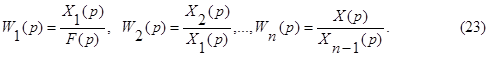
По определению эквивалентной передаточной функции содинения
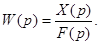
Перемножая левые и правые части равенства (23), получим
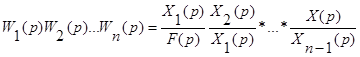
или
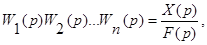
т.е.
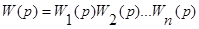 .
.
Передаточная функция последовательно соединенных элементов равна произведению передаточных функций отдельных элементов.
2.Параллельное соединение звеньев. При этом соединении входные сигналы одинаковы, а выходные – суммируются (см. рис.32)
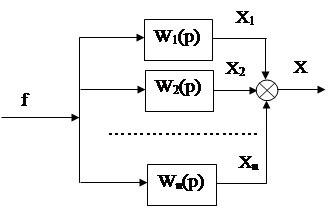 |
Рис.32
Передаточные функции элементов определяются соотношениями
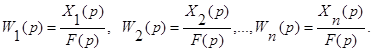
Эквивалентная передаточная функция определяется формулой
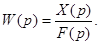
По условию соединения
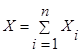
и тогда
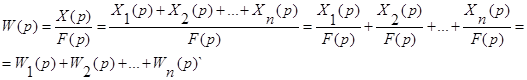
Таким образом,
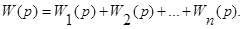
Передаточная функция параллельного соединения равна сумме передаточных функций отдельных звеньев.
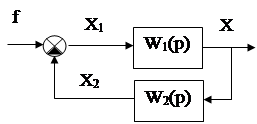 |
3.Обратное соединение. Это соединение, при котором выход второго элемента соединяется со входом первого элемента (см. рис.33). Обратная связь – отрицательная.
Рис.33
В этом соединение можно выделить прямую цепь с передаточной функцией W1(p) (это может быть эквивалентная передаточная функция) и обратную связь с передаточной функцией W2(p). Определим передаточную функцию всего соединения.
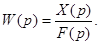
Для отдельных звеньев и элементов соединения имеем
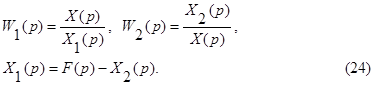
Проведем исключение промежуточных переменных X1(p), X2(p):
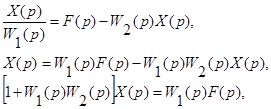
откуда получаем
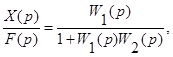
т.е. 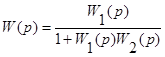 .
.
Это выражение для эквивалентной передаточной функции соединения с отрицательной обратной связью. Для случая положительной обратной связи последнее уравнение (24) имеет вид
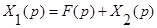
и эквивалентная передаточная функция соединения определяется зависимостью
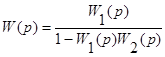 .
.
Произведение W1(p)W2(p) представляет собой передаточную функцию разомкнутой системы. Таким образом, эквивалентная передаточная функция обратного соединения представляет собой дробь, в числителе которой стоит передаточная функция прямой цепи, а в знаменателе – передаточная функция разомкнутой системы, взятая со знаком ”плюс” для случая отрицательной обратной связи и со знаком “минус” для случая положительной обратной связи и увеличенная на единицу.
Правило переноса точки съема.
Если точка съема переносится в направлении, противоположном направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями, расположенные на пути между прежней и новой точками (см. рис.34).
 |
Рис.34
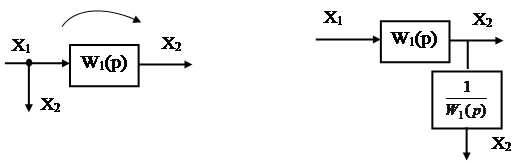 |
Если точка съема переносится в направлении прохождения сигнала, то в переносимую ветвь нужно включить элементы с обратными передаточными функциями всех звеньев, расположенные на пути между прежней и новой точками (см. рис.35).
Рис.35
Правила переноса точки суммирования.
Если точка суммирования переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями всех звеньев, встречающихся между прежней и новыми точками (см. рис.36).
 |
Рис.36
Если точка суммирования переносится в направлении, противоположном направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями, расположенные на пути между прежней и новой точками (см. рис.37).
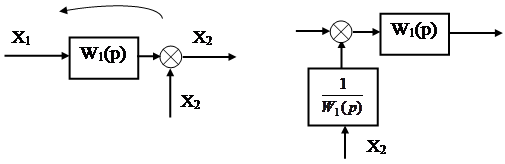 |
Рис.37
Общая методика определения эквивалентных передаточных функций сложных систем состоит в следующем:
1.вводим вспомогательные переменные, принимая за них входы элементов сравнения и отдельных звеньев системы.
2.Рассматривая отдельные части схемы, составляем систему уравнений относительно вспомогательных переменных, входной и выходной переменных САУ.
3.Исключаем вспомогательные элементы и записываем уравнение относительно входной и выходной переменных САУ.
4.Записываем эквивалентную передаточную функцию.
Пример.
Пример. Найти эквивалентную передаточную функцию САУ со следующей структурной схемой
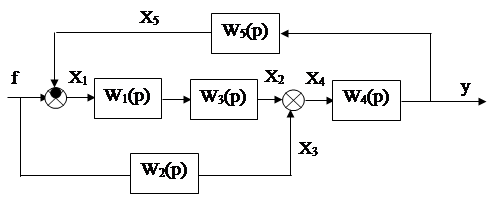 |
Рис.38
1.Вводим вспомогательные переменные X1-X5.
2.Записываем систему уравнений
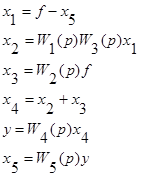 .
.
3. Исключаем вспомогательные переменные :

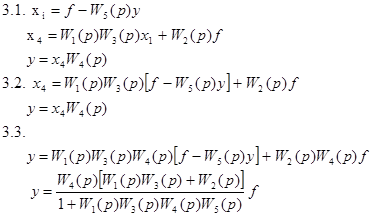
4.
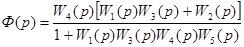 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Решение дифференциальных уравнений линейных стационарных САУ. Свободный и вынужденный режим движения САУ. | | | Передаточные функции различных систем. |
Дата добавления: 2017-10-04; просмотров: 6538;











