ВЧХ скомпенсированной системы должна удовлетворять условию

.

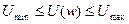Для этого желаемая ЛАЧХ разомкнутой системы должны удовлетворять условию

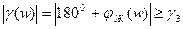, (141)

.

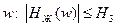7.Соединяем низкочастотную и среднечастотную асимптоты отрезками с наклонами, кратными 20 дб/дек так, чтобы в интервал частот, где

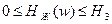
выполнялось условие (141). Проверка условия (141) выполняется либо непосредственным построением ЛФЧХ либо по приближенной формуле

,

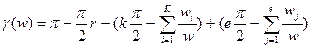где К – число сопрягаемых частот, где наклон уменьшается на – 20 дб/дек,

w_i – значения этих сопрягаемых частот,

е – число сопрягаемых частот, где наклон увеличивается на + 20 дб/дек,

w_j – значения этих частот.

Обычно наклон отрезка, соединяющего низкочастотную и среднечастотную асимптоты, не превышает – 40 дб/дек. Если наклон получается больше – 40 дб/дек, то сопряжение проводят несколькими отрезками так, чтобы разница между наклонами соседних отрезков не превышала 20 дб/дек (см. рис.110)

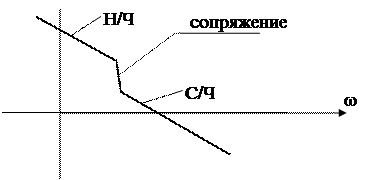Рис.110

8. Сопрягаем среднечастотную и высокочастотную части желаемой ЛАЧХ так, чтобы в интервале частот, где

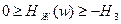
выполняется условие (141). Проверка выполнения условия (141) проводится либо построением ЛФЧХ системы либо использованием приближенной формулы

,

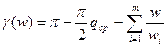где q_cp – коэффициент, учитывая наклон среднечастотной части желаемой ЛАЧХ ; при наклоне – 20 дб/дек q_cp=1,

m – число часто сопряжения, больших частоты среза,

w_i – значения частот сопряжения.

При этом предполагается, что при каждом значении w_i наклон ЛАЧХ уменьшается на – 20 дб/дек.

Пример. Построить желаемую ЛАЧХ системы. Передаточная функция исходной разомкнутой САУ имеет вид

.

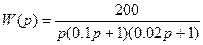Требования к скорректированной системе следующие:

1. Время переходного процесса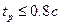

2. Перерегулирование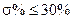

3. Максимальное значение второй производной управляемой величины не должно превышать 80[1/c²] при входном сигнале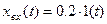

4. Порядок астатизма r=1.

Построение желаемой ЛАЧХ выполняется в следующем порядке.

1. Строится ЛАЧХ неизменяемой части системы (располагаемую ЛАЧХ), так как требования по точности специально не оговариваются, то коэффициент передачи разомкнутой системы при этом остается неизменным. Построенная ЛАЧХ показана на рис.111.

Рис.111

2. Выбираем частоту среза желаемой ЛАЧХ. Находим

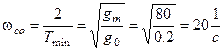
Определим w_см. На монограмме рис.. значению s%=30% соответствует 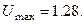Из графика 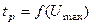по известному значению 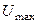найдем

,

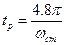откуда

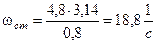
Таким образом, w_с должна находиться на отрезке [18,8; 20]

Выберем w_с=19 [1/с].

3. Определим H₃,g₃. Имеем 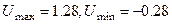. По номограмме замыкания для ВЧХ находим H₃=11 дб,g₃=35^о.

4. Сопрягаем низкочастотную и среднечастотные асимптоты отрезков с наклоном –40 дб/дек. Правый конец сопрягающего отрезка помещаем в точку (0,63;13дб) желаемой ЛАЧХ, при этом w₂=4,25 [1/с]. Левую частоту сопряжения w₁ определяем как точку пересечения отрезка с низкочастотной асимптотой располагаемой ЛАЧХ, w₁=0,12 [1/с].

Проверяем выполнение условия () по приближенной формуле. Имеем

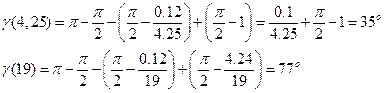
5. Сопрягаем среднечастотную и высокочастотную асимптоты. За частоту сопряжения принимаем w₃=100 [1/с] и w₄=180 [1/с]. Проверяем избыток фазы.

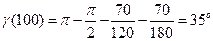
Здесь w=70 [1/с] – частота, при которой H_ж(w)=-11 дб.

На этом построение желаемой ЛАЧХ закончено.

Определение структуры и параметров корректирующего устройства.

Пусть известна желаемая ЛАЧХ и задана передаточная функция разомкнутой нескорректированной системы W_нк(р). Тогда

.

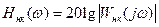Рассмотрим случай, когда коррекция осуществляется последовательным корректирующим устройством с передаточной функцией W_к(p). Тогда ЛАЧХ скорректированной системы определяется как

.

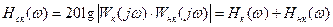С другой стороны ЛАЧХ скорректированной системы должна быть равна желаемой ЛАЧХ, т.е.

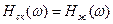
отсюда получим

.

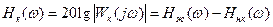Таким образом, синтез последовательного корректирующего устройства осуществляют в следующем порядке:

1. Строим асимптотическую ЛАЧХ нескорректированной системы (располагаемую ЛАЧХ)

2. Строим желаемую ЛАЧХ скорректированной системы.

3. Вычитая из желаемой ЛАЧХ распологаемую, получаем ЛАЧХ корректирующего устройства.

4. Определяем передаточную функцию и подбираем схему и параметры корректирующего устройства.

5. Проверяем, удовлетворяет ли скорректированная система предъявляемым к ней требованиям.