Классификация САУ. Математическое описание линейных стационарных САУ.

Классификация САУ.

Классификация САУ может проводиться по ряду признаков. Так в зависимости от информации о задающем воздействии САУ делятся на системы стабилизации, программного регулирования и системы зависимого управления. (см. рис. 23)

Рис. 23

В зависимости от установившегося сигнала ошибки системы делятся на статические и астатические. (см. рис.24)

Рис.24

По числу регулируемых величин системы делят на одномерные и многомерные. (см. рис. 25)

Рис. 25

Классификация может осуществляться и по другим признакам. Очевидно, что поведение систем с непрерывным временем дифференциальными уравнениями. Если САУ описываются линейными дифференциальными уравнениями, то такие системы называют линейными. Они могут быть линейными стационарными или нестационарными, с распределенными или сосредоточенными параметрами. (см. рис.26)

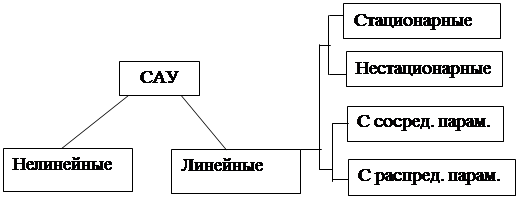Рис.26

В данном курсе основное внимание будет уделено линейным стационарным САУ с сосредоточенными параметрами.

Задачи ТАУ.

Основными задачами ТАУ являются исследования статических (в общем случае установившихся) и динамических свойств САУ и разработка систем удовлетворяющих заданным техническим требованиям.

Исследование процессов работы САУ с заданной структурой, заданными параметрами при различных значениях параметров и различных входных воздействиях составляет содержание задачи анализа. Это задачи оценки устойчивости и определении статических и динамических отклонений, т.е. исследования процессов управления.

Задача синтеза рассматривает построение управляющих устройств, обеспечивающих выполнение требований, предъявляемых к САУ. Здесь проводится выбор схемы управляющего устройства, определение его отдельных элементов и их параметров. Эта задача значительно сложнее задачи анализа.

Математическое описание линейных стационарных САУ.

Системы автоматического управления состоят из отдельных элементов (см. рис.27). Эти элементы имеют входные и выходные величины. Изменение этих величин характеризует работу САУ. Процессы изменения величины описываются дифференциальными уравнениями.

Рис.27

В данном курсе мы будем рассматривать только элементы и системы, описываемые обыкновенными дифференциальными уравнениями, т.е. соотношениями вида

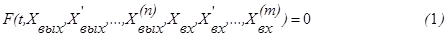
Эта зависимость определяет общий вид дифференциального уравнения. Важный класс систем составляют линейные САУ. Это системы, в состав которых входят только линейные элементы. В свою очередь линейным называют такой элемент, для которого уравнение (1) будет линейным, т.е. оно имеет вид

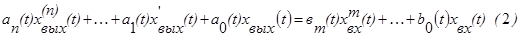
В уравнении (2) коэффициенты a_i, i=0,n, b_j, j=0,m могут быть функциями вермени. Это означает, что свойства элементов с течением времени изменяются. В этом случае говорят о нестационарном линейном элементе. Если в САУ хотя бы один элемент не стационарный, то и вся система не стационарна. Если коэффициенты a_i, i=0,n, b_j, j=0,m – постоянные, то линейные элементы являются стационарными. Система, состоящая из таких элементов, называется линейной стационарной САУ. Именно такие системы мы и будем рассматривать далее.

Таким образом, объектом нашего курса будут линейные стационарные САУ. Это системы, внутренние свойства которых не меняются с течением времени. Такие системы описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Нелинейную систему, описываемую нелинейными дифференциальными уравнениями, стремятся, по крайней мере на начальных этапах исследования свести (приближенно заменить) к близкой к ней линейной системе.

Рассмотрим важнейшее свойство линейных САУ. Пусть X- входная, а Y- выходная величина системы (см.рис. 28).

Рис.28

Дифференциальное уравнение, связывающее X и Y, в общем случае имеет вид

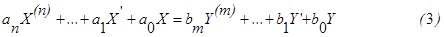
Очевидно (это следует из теории дифференциальных уравнений), что решение этого уравнения X(t) определяется функцией Y(t) (входным задающем воздействием), а также начальными условиями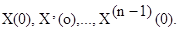

Пусть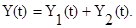

Обозначим X(t) решение уравнения (3), соответствующее входному сигналу Y(t) и ненулевым начальным условиям

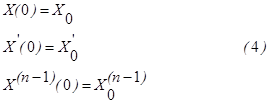
Обозначим X_н(t)-решение (3), соответствующее Y(t)º0 и начальным условиям (4), X₁(t)- решение (3), соответствующее входному сигналу Y₁(t) и нулевым начальным условиям, X₂(t)- решение (3) при входном сигнале Y₂(t) и нулевых начальных условиях, X₃(t)- решение (3), соответствующее Y(t) и нулевым начальным условиям. Тогда

Выражение (5) выражает собой принцип суперпозиции. Из него следует, что реакция системы на внешнее воздействие равно той же линейной комбинации реакции системы на каждое воздействие. Из (6) следует, что для определения процесса на выходе САУ при наличии сигнала на входе и ненулевых начальных условиях можно отдельно рассчитать процессы, соответствующие входному сигналу и начальным условиям, после чего общий процесс определяется как сумма этих реакций.

Использование этих свойств существенно облегчает исследование линейных САУ.