Построение желаемой ЛАЧХ.
Построение желаемой ЛАЧХ основывается, во-первых, на свойствах оптимальных характеристик и, во-вторых, на связи переходного процесса с ВЧХ системы. При этом задающее воздействие полагается ступенчатым и учитываются следующие требования, предъявляемые к системе:
-время регулирования tp max,
-перерегулирование s%,
-максимальное значение второй производной регулируемой величины по времени gm,
-установившееся значение регулируемой величины,
-порядок астатизма скорректированной системы r.
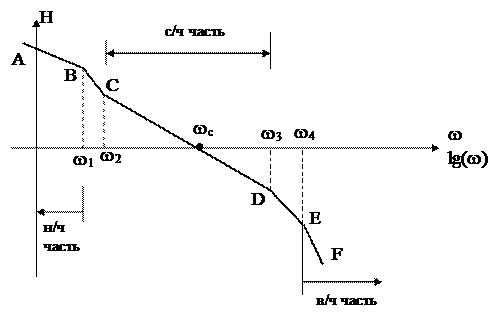 |
При построении желаемой ЛАЧХ в первом приближении будем считать, что она может быть заменена асимптотами. В ЛАЧХ условно можно выделить низкочастотную, среднечастотную и высокочастотную части (см. рис. 104.)
Рис.104
Здесь АВ - низкочастотная, CD - среднечастотная, EF - высокочастотная части ЛАЧХ.
Основные правила построения желаемой ЧХ.
Основные правила построения желаемой ЛАЧХ заключаются в следующем:
1. Определяем значение коэффициента передачи разомкнутой скорректированной системы. Оно находится исходя из величины ошибки, возникающей из-за наличия задающего или возмущающего воздействия.
Ошибка воспроизведения задающего воздействия
а) статическая система, постоянное воздействие:
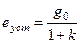
Если необходимо, чтобы было
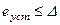 ,
,
то величина k должна удовлетворять условию

б) астатическая система, постоянное воздействие
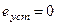
и 
в) астатическая система, задающее воздействие vt. Тогда
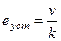
и, если 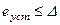 , то
, то

г) гармоническое входное воздействие с амплитудой А и частотой 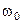
 .
.
Если необходимо, чтобы Ае<D, то ЛАЧХ скорректированной системы должна удовлетворять условию
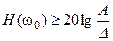 .
.
Ошибка, вызванная возмущающим воздействием, зависит от структурной схемы системы и места приложения воздействия. Однако обычно в результате получаем условие 
Где kгр – некоторое граничное значение. С учетом полученныхдля конкретной системы условий (135) – (138) окончательно выбирается значение К коэффициента передачи разомкнутой системы.
2.Строим ЛАЧХ исходной (нескорректированной системы) с коэффициентом передачи, найденным в п.1.Пусть
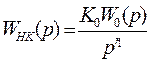
где К0 – коэффициент передачи нескорректированной САУ
W0(p) – дробно-рациональная передаточная функция и W0(0)=1,
r1 – порядок астатизма нескорректированной САУ.
 |
При построении ЛАЧХ рассматривается передаточная функция
 (139)
(139)
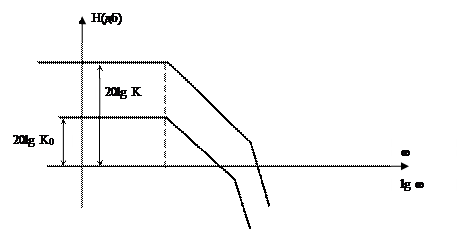
с измененным значением коэффициента передачи.(см. рис.105).
Рис.105
3.Строим низкочастотную и высокочастотную части желаемой ЛАЧХ. Низкочастотная часть строится, исходя из выбранного значения К и заданного порядка астатизма разомкнутой системы r. Уравнение низкочастотной асимптоты желаемой ЛАЧХ имеет вид
HHЧ(w)=20lgK – 20r lg w,
т.е. низкочастотная асимптота имеет наклон – 20r дб/дек.
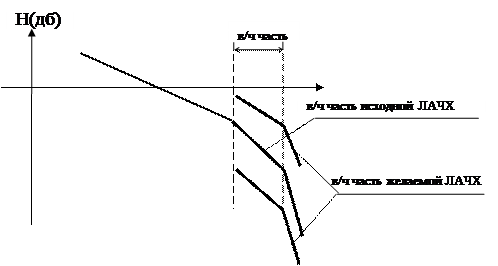 |
Высокочастотная часть должна совпадать с высокочастотной частью ЛАЧХ, соответствующей передаточной функции (139) или проходить параллельно ей (см. рис. 106). Это обеспечивает максимальную простоту реализации корректирующего устройства.
Рис.106.
4.Строим среднечастотную часть желаемой ЛАЧХ с наклоном – 20дб/дек. (см. рис.107). Частота среза определяется из условия
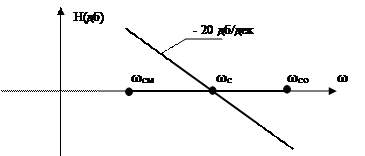 |
Рис.107.
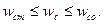 (140)
(140)
В (140) wcm – минимальная частота среза, определяемая по времени регулирования,
wco – частота среза оптимальной системы.
Для определения wco используется равенство
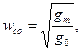
в котором величины gm, g0 являются исходными данными для синтеза. Выполнение условия
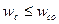
гарантирует, что в переходном процессе ускорение 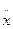 не превысит gm.
не превысит gm.
Значение wcm определяется с помощью рассмотренных ранее номограмм (см. рис.108), построенных для определенного типа ВЧХ.
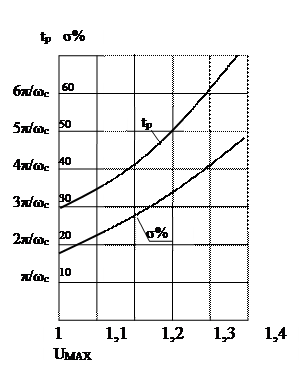 |
Рис.108.
По заданному перерегулированию определяем Umax и далее 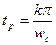 . Из последнего выражения имеем
. Из последнего выражения имеем
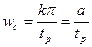
и, приравнивая время регулирования заданному, получим минимальное значение частоты среза
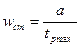 .
.
При выполнении условия
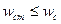
время переходного процесса не превосходит заданное.
В некоторых случаях возможно, что
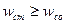
| <== предыдущая лекция | | | следующая лекция ==> |
| Синтез корректирующих устройств САУ методом ЛАЧХ. | | | ВЧХ скомпенсированной системы должна удовлетворять условию |
Дата добавления: 2017-10-04; просмотров: 6438;











