Анализ точности и качества линейных систем автоматического регулирования (продолжение).

Гармонический входной сигнал.

3.Рассмотрим ту же систему при гармоническом входном сигнале

.

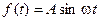При рассмотрении АФЧХ САУ было показано, что вынужденный процесс x_в(t) также является гармоническим и

,

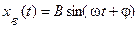где .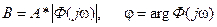

Таким образом, мы определили вид вынужденных процессов при наиболее распространенных входных воздействиях.

Рассмотрим теперь точность системы в типовых режимах. Пусть кроме управляющего к системе прикладывают возмущающее воздействие g(t). Структурная схема САУ имеет вид (см. рис. 81.). Ошибка e(t)

Рис.81

определяется выражением

.

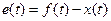Имеем из структурной схемы

.

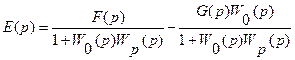Пусть 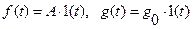. Тогда

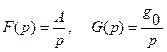
и

,

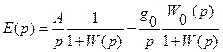где 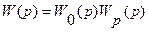- передаточная функция разомкнутой системы. По теореме о предельном переходе (мы считаем, что замкнутая САУ устойчива и эту теорему можно применять) имеем

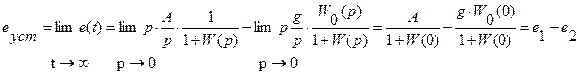
где 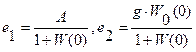, e₁ – составляющая ошибки, определяемая задающим воздействием f(t), e₂ – составляющая ошибки, определяемая возмущающим воздействием.

Рассмотрим составляющую e₁:

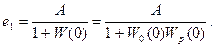
В случае статической системы W(0)=K и тогда

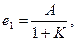(83)

где К коэффициент передачи разомкнутой системы. Из (83) видно, что величина е₁ уменьшается с ростом К. Поэтому с точки зрения повышения точности системы увеличение К выгодно. Однако оно ограничивается требованиями устойчивости, поэтому на практике приходиться искать компромисс между устойчивостью и точностью САУ.

Из (83) также следует, что если задано условие

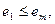
e_м - максимально допустимая величина ошибки при заданном входном сигнале, то отсюда следует

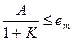
и тогда

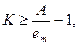(84)

при этом неравенство (84) определяет допустимый с точки зрения точности диапазон значений коэффициента передачи разомкнутой системы.

Если передаточная функция W(p) имеет астатизм, т.е. содержит интегрирующие звенья, то W(0)=∞ и е₁ =0, т.е. в астатических системах ошибка, определяемая постоянным задающим воздействием, отсутствует.

Рассмотрим составляющую е₂:

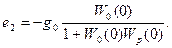
Если передаточная функции объекта и регулятора не содержат интегрирующих звеньев (астатизм отсутствует ), то W₀(0)=K₀ , W_p(0)=K_p и

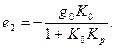
Из полученного выражения видно, что при возрастании К_р величина 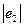уменьшается, при увеличении К₀ 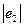возрастает.

Астатическая система.

В астатической системе W(0)=∞ , однако величина е₂ зависит от того где именно находиться интегрирующее звено: в объекте управления или в регуляторе.

а) астатизм в объекте управления, т.е. W₀(0)=∞, W_p(0)=K_p≠0.

Тогда

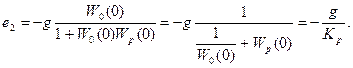
Абсолютная величина ошибки уменьшается с увеличением коэффициента передачи регулятора, но она отлична от нуля.

б) астатизм в регуляторе, т.е. W_p(0)=∞. При этом

е₂=0 .

Таким образом, если интегрирующий элемент включен в цепь между сигналом ошибки и точкой приложения возмущающего воздействия, то составляющая ошибки е₂=0. Если интегратор включен между точкой приложения возмущающего воздействия и выходом системы, то е₂≠0.