Дифракция Фраунгофера от щели.

Немецкий физик И. Фраунгофер A787— 1826) рассмотрел дифракцию плоских световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

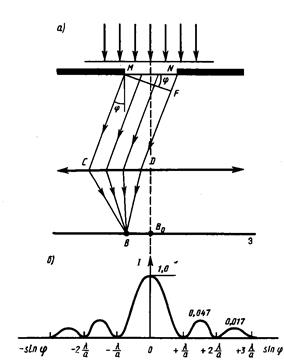Рис.9.2

Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 9.2, а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j,

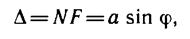(9.1)

где F — основание перпендикуляра,

опущенного из точки М на луч ND (волновая поверхность MF).

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна l/2, т. е. всего на ширине щели уместится 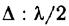зон. Так как свет на щель падает нормально, то плоскость щели совпадает с фронтом волны; следовательно, все точки фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Из выражения 9.1 вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно погашают друг друга. Следовательно, если число зон

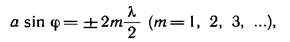9.2,

Френеля четное, то в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное

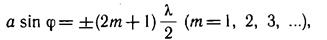9.3

то наблюдается дифракционный максимум, соответствующий действию одной не скомпенсированной зоны Френеля. Отметим, что в прямом направлении (j= 0) щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке S_o наблюдается центральный дифракционный максимум.

Из условий 9.2 и 9.3 можно найти направления на точки экрана, в которых амплитуда (а, следовательно, и интенсивность) равна нулю

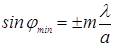9.4

или максимальна

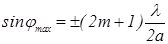9.5

Распределение интенсивности на экране, получаемое следствие дифракции (дифракционный спектр), приведено на рис. 9.2б. Расчеты показывают, что интенсивности центрального и последующих максимумов относят как 1:0,047:0,017:0,0083:..., т. е. основная часть световой энергии сосредоточена центральном максимуме. Из опыта и соответствующих расчетов следует, что

сужение щели приводит к тому, что центральный максимум расплывается, а его яркость уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире (а>l,), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При а>>l. в центре получается резкое изображение источника света, т. е. имеет место прямолинейное распространение света. Положение дифракционных максимумов зависит от длины волны l, поэтому рассмотренный вид дифракционная картина имеет лишь для монохроматического света. При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех длин волн (при j = 0 разность хода равна нулю для всех l). Боковые максимумы радужно окрашены, так как условие максимума при любых m различно для разных l. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m=1), второго (m = 2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.