Дифракция Френеля и Фраунгофера
Рассмотрим распределение интенсивности в дифракционной картине от круглой щели. На предыдущей лекции мы рассмотрели формирование максимумов и минимумов в центре дифракционной картины.
Заметим, что без экрана с отверстием амплитуда поля в точке наблюдения равна 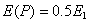 . Таким образом, благодаря явлению дифракции света на экране с отверстием, открывающем небольшое нечётное число зон Френеля, наблюдается увеличение интенсивности падающего на него света почти в два раза., Преграда с отверстием, открывающим небольшое нечетное число зон, не только не ослабляет освещенность в точке Р, но, напротив, приводит к увеличению амплитуды почти в два раза, а интенсивности — почти в четыре раза.
. Таким образом, благодаря явлению дифракции света на экране с отверстием, открывающем небольшое нечётное число зон Френеля, наблюдается увеличение интенсивности падающего на него света почти в два раза., Преграда с отверстием, открывающим небольшое нечетное число зон, не только не ослабляет освещенность в точке Р, но, напротив, приводит к увеличению амплитуды почти в два раза, а интенсивности — почти в четыре раза.
 8.13
8.13
|
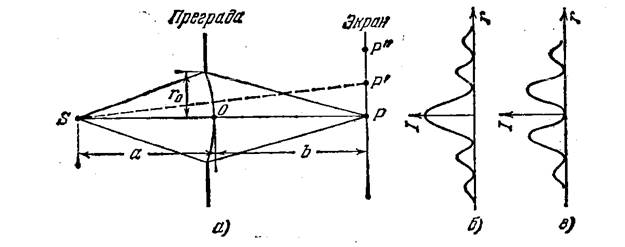
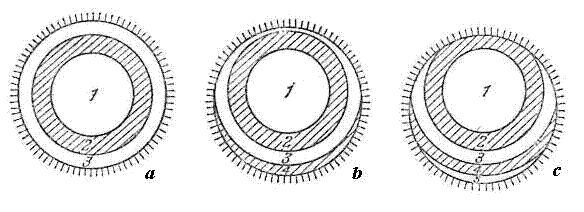
Выясним характер дифракционной картины, которая будет наблюдаться на экране, помещенном за преградой (см. рис. 8.11). Вследствие симметричного расположения отверстия относительно прямой SP освещенность в разных точках экрана будет зависеть только от расстояния г от точки Р. В самой этой точке интенсивность будет достигать максимума или минимума в зависимости от того, каким — четным или нечетным — будет число открытых зон Френеля. Пусть, например, это число равно трем. Тогда в центре дифракционной картины получится максимум интенсивности. Картина зон Френеля для точки Р дана на рис. 8.13, а. Теперь сместимся по экрану в точку Р'. Ограниченная краями отверстия картина зон Френеля для точки Р' имеет вид, показанный на рис. 8.13, б. Края отверстия закроют часть третьей зоны, одновременно частично откроется четвертая зона. В итоге интенсивность света уменьшится и при некотором положении точки Р' достигнет минимума. Если сместиться по экрану в точку Р", края отверстия частично закроют не только третью, но и вторую зону Френеля, одновременно откроется частично пятая зона (рис. 8.13 в). В итоге действие открытых участков нечетных зон перевесит действие открытых участков четных зон, и интенсивность достигнет максимума, правда, более слабого, чем максимум, наблюдающийся в точке Р. Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец. В центре картины будет либо светлое (m нечетное), либо темное.(8.14)
Рассмотрим вид дифракционной картины в зависимости от размера отверстия.
 Рис.8.14
Рис.8.14
|
Если размер отверстия во много раз меньше первой зоны Френеля, то наблюдается размытое светлое пятно без каких либо колец. Если отверстие открывает 'много' зон Френеля, то дифракционные кольца наблюдаются в узкой области на границе свет тень. А в остальной части экрана наблюдается практически равномерное освещение экрана, за исключением области геометрической тени, где освещённость отсутствует.
Дифракция на диске.
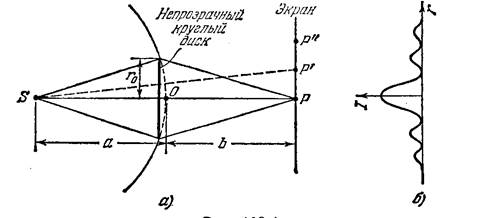 Рис.15
Рис.15
|
Пусть свет из точки источника 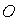 (рис. 8.15) освещает непрозрачный диск радиуса
(рис. 8.15) освещает непрозрачный диск радиуса 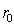 , за которым на прямой, перпендикулярной плоскости диска и проведенной через его центр, располагается точка наблюдения
, за которым на прямой, перпендикулярной плоскости диска и проведенной через его центр, располагается точка наблюдения 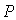 . Как и выше, будем считать, что размер диска во много раз меньше расстояний от диска до источника a и от диска до точки наблюдения
. Как и выше, будем считать, что размер диска во много раз меньше расстояний от диска до источника a и от диска до точки наблюдения 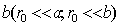 .Предположим, что диск из точки наблюдения
.Предположим, что диск из точки наблюдения 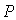 закрывает
закрывает 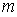 зон Френеля. Тогда амплитуда света
зон Френеля. Тогда амплитуда света 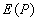 в точке наблюдения будет равна алгебраической сумме амплитуд волн
в точке наблюдения будет равна алгебраической сумме амплитуд волн 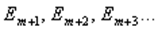 открытых зон Френеля:
открытых зон Френеля:
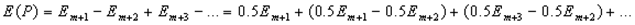 Учитывая, что амплитуды зон Френеля образуют убывающий ряд с чередующимся знаком, однотипные выражение в скобках можно положить равными нулю, и тогда получим
Учитывая, что амплитуды зон Френеля образуют убывающий ряд с чередующимся знаком, однотипные выражение в скобках можно положить равными нулю, и тогда получим
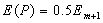 (8.15)
(8.15)
Отсюда следует, что в центре дифракционной картины, создаваемой диском, всегда наблюдается светлое пятно, независимо от размеров диска. В истории физики это свойств зон Френеля явилось доказательством волновой природы света. С точки зрения современников Френеля наблюдение светлого пятна в центре геометрической тени препятствия, освещаемого светом, казалось абсурдным, что и послужило основанием для Пуассона (1781-1853) возразить против волновой природы света. Для проверки этого возражения Араго (1786-1853) поставил опыт, которым действительно наблюдалось светлое пятно в центре геометрической тени диска (рис. 8.16), освещаемого светом, получившее название пятно Араго- Пуассона. Справедливости ради, необходимо отметить, что наблюдение пятна было отмечено задолго до опыта Араго - ещё в 1713г. Делилем, а 1723г. Моральди. Однако, поскольку природа этого явления была непонятна, то наблюдения оказались незамеченными.
Дифракционная картина от диска, наблюдаемая на экране (рис8.16), имеет характер чередующихся тёмных и светлых колец, в центре которых находится светлое пятно.
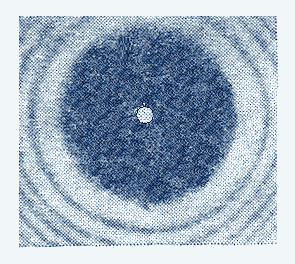 Рис.8.16
Рис.8.16
|
Выясним характер картины, получающейся на экране (см. рис. 8.15) Очевидно, что освещенность может зависеть только от расстояния г до точки Р. При небольшом числе закрытых зон амплитуда 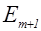 мало отличается от
мало отличается от 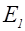 Поэтому интенсивность в точке Р будет почти такая же, как при отсутствии преграды между источником S и точкой Р
Поэтому интенсивность в точке Р будет почти такая же, как при отсутствии преграды между источником S и точкой Р 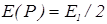 Для точки Р', смещенной относительно точки Р в любом радиальном направлении, диск будет перекрывать часть (m+1)-й зоны Френеля, одновременно откроется часть m-й зоны. Это вызовет уменьшение интенсивности. При некотором положении точки Р' интенсивность достигнет минимума. Если сместиться из центра картины еще дальше, диск перекроет дополнительно часть (m+2)-й зоны, одновременно откроется часть (m—1)-й зоны. В результате интенсивность возрастет и в точке Р" достигнет максимума.
Для точки Р', смещенной относительно точки Р в любом радиальном направлении, диск будет перекрывать часть (m+1)-й зоны Френеля, одновременно откроется часть m-й зоны. Это вызовет уменьшение интенсивности. При некотором положении точки Р' интенсивность достигнет минимума. Если сместиться из центра картины еще дальше, диск перекроет дополнительно часть (m+2)-й зоны, одновременно откроется часть (m—1)-й зоны. В результате интенсивность возрастет и в точке Р" достигнет максимума.
Рассуждения, очевидно, справедливы для диска, открывающего произвольное число (не очень большое) чётных или нечётных зон Френеля.
Таким образом, амплитуда волны в центре дифракционной картины от диска любого размера равна половине амплитуды волны от первой открытой зоны Френеля, что совпадает с результатом проведенных выше расчётов. На периферии дифракционной картины от диска распределение интенсивности в основном определяется амплитудой волны источника, на которую 'накладываются' затухающие по мере удаления от центра картины колебания волн от частично открытых зон Френеля отверстием в непрозрачном экране того же диаметра, что и рассматриваемый диск.
Рассмотрим вид дифракционной картины в зависимости от размера диска. Если размер диска во много раз меньше первой зоны Френеля, то наблюдается практически равномерное освещение экрана - диск как бы не отбрасывает тени. Если размер диска закрывает 'много' зон Френеля, в центре дифракционной картины светлого пятна практически не видно т.к. 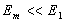 , освещённость картины в области геометрической тени практически равна нулю, а дифракционные кольца наблюдаются в узкой области на границе свет тень.
, освещённость картины в области геометрической тени практически равна нулю, а дифракционные кольца наблюдаются в узкой области на границе свет тень.
Дата добавления: 2017-10-04; просмотров: 2687;











