Вопрос 2. Принцип Гюйгенса-Френеля. Зоны Френеля.

Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Однако этот принцип не позволяет вычислить амплитуду (интенсивность) волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением об интерференциивторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый таким образом принцип Гюйгенса получил название принципа Гюйгенса - Френеля:все источники вторичных волн,расположенные на поверхности фронта волны, когерентны между собой; световая волна в любой точке пространства является результатом интерференции волн, излучаемых вторичными источниками и достигших этой точки. При этом предполагается, что вторичные волны излучаются только вперед, а возможность возникновения обратных вторичных волн исключается. Поскольку точек фронта, являющихся когерентными источниками новых волн,бесчисленное множество, то расчет интерференции сводится к довольно громоздкому интегрированию. Для упрощения решения этого вопроса Френелем был предложен метод разделения фронта волны на зоны таким образом, что волны от соседних зон приходят в точку наблюдения в противоположной фазе и ослабляют друг друга. С методом зон Френеляознакомимся на примере дифракции сферической световой волны на непрозрачной преграде.

Пусть S - точечный источник монохроматического света, распространяющегося в однородной среде. По принципу Гюйгенса от него распространяется во все стороны сферическая волна. В некоторый момент времени фронт этой волны занимает положение Ф, рис.9.2. Рассмотрим произвольную точку Р перед фронтом волны и соединим её прямой линией с источником света S . Волновые поверхности будут симметричны относительно прямой SР.

Рис.9. 2.

Если бы свет распространялся прямолинейно вдоль луча SОР, то достаточно было бы поставить на его пути сколь угодно малый экран 1, чтобы в точке наблюдения Р была полная темнота. Благодаря волновой природе света в точку Р приходят волны не только от точки О, но и от всех остальных точек фронта Ф, правда, в различных фазах.

Для расчета результатов интерференции Френель предложил провести ряд сфер с центрами в точке Р и радиусами, соответственно равными

b +l/2,

b + 2l/2,

b + 3l/2, и т.д.

Тем самым фронт волны Ф разобьется на ряд кольцевых зон, рис.9.2. Здесь зоны Френеля являются иточниками вторичных волн и в соответствии с принципом Гюйгенса-Френеля излучают свет в основном в направлении внешней нормали. Волны, приходящие в точку P от точек каждой последующей зоны, сдвинуты по отношению к волнам, приходящим от соответствующих точек предыдущей зоны, на λ/2, т.е. находятся в противоположных фазах, и их амплитуды при интерференции вычитаются. Из геометрического рассмотрения можно получить выражение для радиуса внешней границы m - ой зоны:

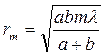, (m = 1, 2, 3, …). (9.1)

Если, например, а = b = 1 м и λ = 0,5 мкм, то радиус первой зоны

r₁ = 0,5 мм.

Занумеруем величины суммарных амплитуд волн, приходящих в точку Р от каждой последующей зоны: А₁, А₂, а₃, А₄, А₅, А₆, ....

Благодаря различию в расстояниях зон до точки наблюдения и в углах, под которыми видны эти площадки из точки Р, величины этих амплитуд монотонно убывают:

А₁> А₂> а₃> А₄> А₅> А₆, ....

т.е. в соответствии с принципом Гюйгенса- Френеля вторичные источники (зоны Френеля) излучают свет в основном направлении внешней номали и формула (9.2) есть следствие того, что амплитуда А_i − монотонно убывающая функция.

В качестве допустимого приближения можно принять, что амплитуда колебания от некоторой k-той зоны Френеля А_k равна среднему арифметическому от амплитуд примыкающих к ней зон:

А_k = (А_k+1 + А_k-1)/2. (9.2)

В соответствии с принципом Гюйгенса- Френеля вторичные источники (зоны Френеля) излучают свет в основном направлении внешней номали и формула (9.2) есть следствие того, что амплитуда А_i − монотонно убывающая функция.

Амплитуда результирующего светового колебания в точке Р, равна сумме амплитуд, создаваемых каждой отдельной зоной. При этом амплитуды от всех четных зон надо складывать с одинаковым знаком (например, положительным), а амплитуда волн от всех нечетных зон – с обратным знаком:

А = А₁ - А₂ +А₃ - А₄ + А₅ -.... (9.3)

Используя (10.2), можно это выражение представить в виде

А = А₁/2 + (А₁/2 – А₂ +А₃/2) + (А₃/2 –А₄ + А₅ /2) + ... » А₁/2, (9.4)

так как оставшаяся часть от амплитуды последней зоны ± А_k/2мала.

Таким образом при большом числе открытых зон Френеля амплитуда от воздействия всего фронта Ф в точке наблюдения Р, равная А = А₁/2,эквивалентна половине воздействия центральной зоны Френеля, т.е. распространение света от источника S в точку наблюдения Р происходит так, будто свет распространяется прямолинейно вдоль направления SР. Значит, волновое описание процесса распространения света не противоречит закону прямолинейного распространения света в однородной среде, используемого в геометрической оптике.