Частные случаи моментов инерции

·Момент инерции однородного тонкого стержня массы М длиной l относительно оси, проходящей через конец стержня перпендикулярно к нему (рис.24).

Используя соотношение (3.11) и учтя, что 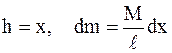, получим:

.
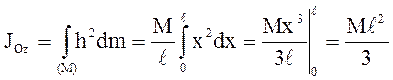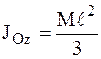. (3.17)

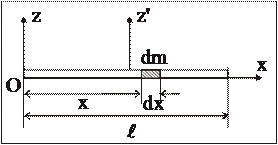
Рис. 24

Если ось z' проходит через середину стержня, то, изменив пределы интегрирования, несложно получить:

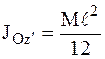. (3.18)

· Момент инерции однородной окружности (тонкого кольца) массы М радиуса r относительно оси, проходящей через центр окружности перпендикулярно ее плоскости (рис. 25).

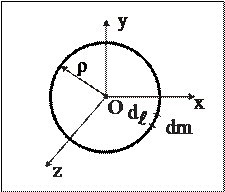
Рис. 25

Используя соотношение (3.11) и учтя, что

,

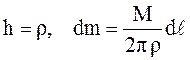получим:

.

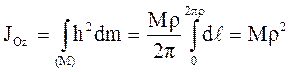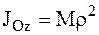. (3.19)

Момент инерции однородного кругового полого цилиндра относительно его оси определяется также по соотношению (3.19).

· Момент инерции однородного тонкого диска массы М радиуса r относительно оси, проходящей через его центр перпендикулярно его плоскости (рис. 26).

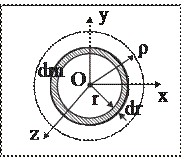
Рис. 26

Используя соотношение (3.11) и учтя, что

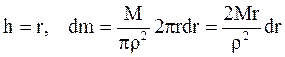
( – площадь бесконечно тонкого кольца), получим:

.
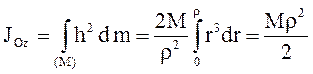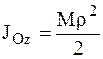. (3.20)

Момент инерции однородного круглого сплошного цилиндра относительно его оси определяется также соотношением (3.20).

· Радиус инерции. В случае сложной конфигурации НМС его момент инерции определяется экспериментально и может быть выражен через радиус инерции. В этом случае момент инерции определяется по формуле:

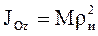, (3.21)

где ­­­­­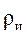– радиус инерции.