Неравномерное вращение. Понятие о моменте инерции

Говоря о движении тела по окружности, мы имели в виду такое движение, при котором скорость тела во всех точках окружности все время остается постоянной. Такое вращательное движение называется равномерным вращением. Если же при движении но окружности скорость в различных ее точках не остается постоянной, а меняется (увеличивается или уменьшается), то такое вращательное движение называется неравномерным вращением.

Например, при запуске мотора самолета винт вращается неравномерно (число оборотов увеличивается); при работе мотора на одних и тех же оборотах скорость вращения винта будет постоянной, и, следовательно, вращение будет равномерное; при уменьшении числа оборотов мы будем иметь, очевидно, снова неравномерное вращение.

Из предыдущего мы знаем, что тело приходит во вращательное движение под действием ничем не уравновешенного момента силы или момента пары сил (см. § 7 и 8). _г Чем больше момент действующей силы (или пары сил), тем быстрее тело будет вращаться. Однако под действием одного и того же момента силы тело будет вращаться с различной скоростью, если мы будем помещать массу тела на разных расстояниях от оси вращения. В этом легко убедиться, если воспользоваться вертушкой, изображенной на рис. 37.

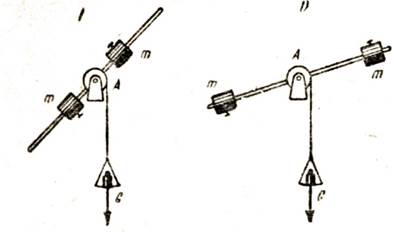
Рис. 37. Момент инерции тела тем больше, чем дальше находится масса от оси вращения

Вертушку приводит во вращение гиря G с помощью нити и шкива А, насаженного на ось вращения. Таким образом, вращающий момент силы G будет равен произведению силы G на радиус шкива. Под действием вращающего момента силы G вертушка начнет вращаться с некоторой скоростью (рис. 37, I); если же грузы mm закрепить дальше от оси вращения (рис. 37, II), то пол действием того же момента силы G вертушка начнет вращаться с меньшей скоростью.

В обоих случаях вращающий момент силы один и тот же и масса вертушки (масса всей вращающейся системы) одна и та же, однако во втором случае привести во вращение систему труднее, чем в первом. Как же это объяснить?

Объясняется это тем, что во втором случае инертность нашей системы больше, чем в первом. Таким образом, инертность тела зависит не только от массы тела, но и от ее расположения: чем дальше находится масса от оси вращения, тем труднее привести тело во вращательное движение.

Найдено, что, инертность вращающегося тела пропорциональна произведению массы тела на квадрат расстояния от оси вращения. Это произведение называется моментом инерции тела (обозначается буквой I). Следовательно, момент инерции I = mr².

Если тело вращается, делая некоторое число оборотов в единицу времени, то на основании предыдущего можно сказать, что чем больше момент инерции тела, тем труднее изменить его число оборотов, и тем легче, чем больше вращающий момент силы.

Иными словами, изменение числа оборотов в единицу времени пропорционально вращающему моменту силы (М) и обратно пропорционально моменту инерции тела (I). Выражая это математически и учитывая, что изменение числа оборотов в единицу времени называется угловым ускорением (обозначается греч. буквой ε — ‘’эпсилон“), мы можем написать: ε = M/I откуда находим, что вращающий момент силы M = Iε.

Итак, вращающий момент силы равняется моменту инерции, помноженному на угловое ускорение.

Последняя формула выражает второй закон Ньютона применительно к телу, вращающемуся под действием постоянной силы. Сравнивая формулу второго закона для поступательного движения (f = ma) с найденной формулой для вращательного движения (M = Iε), мы видим, что в последней роль силы играет вращающий момент, роль массы-момент инерции, роль ускорения—угловое ускорение.