Общие понятия о цифровой обработке

Под обработкой сигналов в широком смысле можно понимать совокупность преобразований, направленную на наиболее эффективную передачу, хранение и извлечение информации. В последние десятилетия все более широко применяется цифровая обработка сигналов (ЦОС), которой свойственны следующие преимущества перед аналоговой обработкой:

– принципиальная возможность реализации практически любых алгоритмов обработки в реальном масштабе времени (возможности аналоговой техники значительно скромнее);

– потенциально сколь угодно высокая точность реализации алгоритмов, определяемая разрядностью цифровых устройств;

– возможность безошибочного воспроизведения сигналов при передаче и хранении на основе помехоустойчивого кодирования, которое применимо только к цифровым сигналам.

Преимущества цифровой обработки основываются на свойствах дискретных сигналов и цепей, которые во многом сходны с аналоговыми, но в то же время имеют и существенные особенности [7].

Под цифровым сигналом понимают дискретный сигнал, квантованный по уровню.

Математической моделью дискретного сигнала служит последовательность s[n] (дискретный аргумент принято заключать в квадратные скобки), где s – аргумент, принимающий значения из дискретного множества, а функция s[•] может принимать значения из непрерывного множества вещественных или комплексных чисел (в пространственно-временной обработке сигналов функция s[•] принимает векторные значения). В соответствии с теоремой отсчетов, аналоговый сигнал s(t) с финитным спектром, сосредоточенным в полосе частот (-F_в, F_в), может без потерь информации быть заменен дискретной последовательностью s[n] = s(nT_d) своих значений, взятых с шагом T_d < 1/2F_в, которая и представляет собой дискретный сигнал.

Таким образом, цифровой сигнал – это последовательность, принимающая значения из дискретного (как правило, конечного) множества. Это связано с тем, что цифровые устройства всегда имеют ограниченную разрядность и отсчеты сигналов, подлежащих цифровой обработке округляются (квантуются). Для изучения ряда вопросов цифровой обработки сигналов удобнее считать, что сигнал принимает значения из непрерывного множества, поэтому используется модель дискретного сигнала. Моделью цифрового сигнала пользуются в тех случаях, когда рассматриваются специфические эффекты, связанные с квантованием сигнала, округлением промежуточных результатов, ограничением разрядной сетки цифрового устройства и т.п.

Для последовательности (дискретного сигнала) s[n], где n принимает целые значения от -∞ до +∞ можно определить дискретное преобразование Фурье

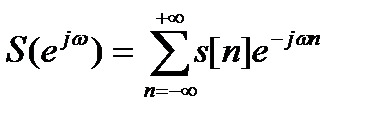, (11.1)

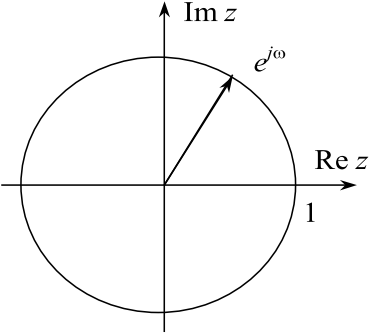Легко заметить, что изменение ω на величину ±k∙2π при любом целом k никак не влияет на результат преобразования. Таким образом, величину ω можно понимать, как угол, а e^jω – как точку на комплексной плоскости, находящуюся на окружности единичного радиуса (рис. 11.1). Поэтому выражение (11.1) определяет на единичной окружности функцию вещественной переменной ω, которая имеет смысл круговой частоты.

Рис. 11.1. Угловая интерпретация частоты

Вспомним, что при восстановлении аналогового сигнала моделью дискретного сигнала служит идеализированный АИМ-сигнал, состоящий из δ-функций, умноженных на отсчеты сигнала

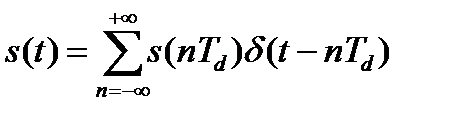
Преобразование Фурье этого аналогового сигнала, обозначив круговую частоту в его спектральном описании буквой Ω, находится как:

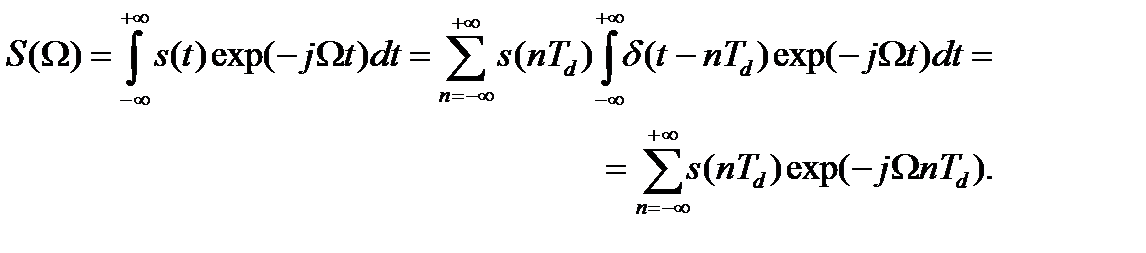(11.2)

Сравнивая выражения (11.1) и (11.2), легко увидеть, что при условии

s[n] = s(nT_d),

ω = ΩT_d, -π ≤ ω ≤ π (11.3)

их левые части совпадают. Это означает, что выражение (11.1) определяет спектральную плотность дискретного сигнала, совпадающую по форме со спектральной плотностью идеального АИМ-сигнала (который при воздействии на идеальный ФНЧ с П-образной характеристикой позволяет точно восстановить исходный аналоговый сигнал).

Из условия (11.3) следует необходимое ограничение -π/T_d ≤ Ω ≤ π/T_d, или, что то же самое, -Ω_d/2 ≤ Ω ≤ Ω_d/2, где Ω_d = 2πF_d = 2π/T_d – круговая частота дискретизации. Иными словами, мы снова получили условие выбора частоты дискретизации, как минимум, вдвое выше верхней частоты спектра аналогового сигнала.

Таким образом, при условии финитности и правильного выбора шага дискретизации, любые действия над дискретным сигналом эквивалентны соответствующим действиям над аналоговым сигналом и обработка сигнала может производиться в цифровой форме.

Рассмотрим выражение (11.1) как разложение 2π-периодической функции аргумента ω в комплексный ряд Фурье по базисным функциям exp(jnω), -∞ ≤ n ≤ ∞. Тогда, очевидно, отсчеты s[n] не что иное, как коэффициенты этого ряда и могут быть найдены по общей формуле для вычисления коэффициентов комплексного ряда Фурье:

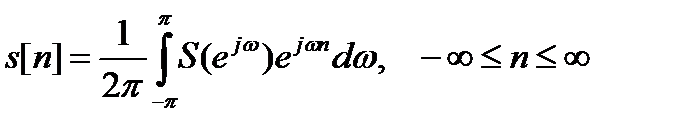, (11.4)

Это выражение представляет собой обратное преобразование Фурье для последовательности (дискретного сигнала).