Временные и спектральные характеристики частотно-манипулированных сигналов

При частотной манипуляции (ЧМн) частота высокочастотного колебания изменяется скачком на величину ±∆f_m относительно несущей f_н (рис. 10.3). Таким образом, на выходе ЧМн вырабатываются колебания на частотах f₁ и f₂.

Разность частот f₁ - f₂ = ∆f_сдв называют частотным сдвигом. Максимальное отклонение частоты ∆f_m от несущей называют девиацией.

Отношение девиации частоты ∆f_m к частоте манипулирующего колебания F называется индексом частотной манипуляции. Индекс ЧМн прямо пропорционален девиации и обратно пропорционален частоте информационного сигнала: m_ЧМн = ∆f_m /F

Различают частотную манипуляцию: с разрывом фазы и без разрыва фазы. Общий вид ЧМн сигнала с разрывом фазы можно представить в виде суммы двух АМн сигналов с разными несущими частотами f₁ и f₂. Технически такой вид манипуляции реализуется с помощью двух генераторов (рис. 10.4), которые управляются ключом под воздействием информационного сигнала: S_ЧМн(t) = S_1АМн(t) + S_2АМн(t).

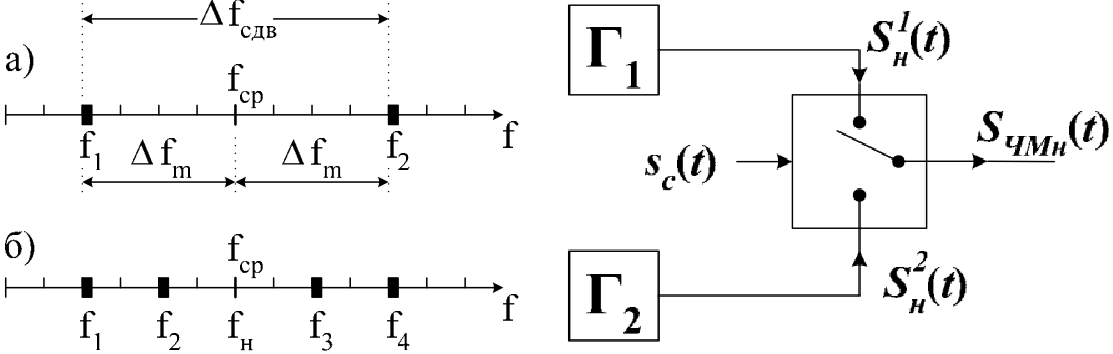
Рис. 10.3. Параметры сигналов Рис. 10.4. Структурная схема

ЧМн с разрывом фазы формирования ЧМн колебаний

Это представление позволяет спектр колебания S_ЧМн(t) найти как результат наложения двух спектров колебаний АМн, который будет иметь вид [5]:

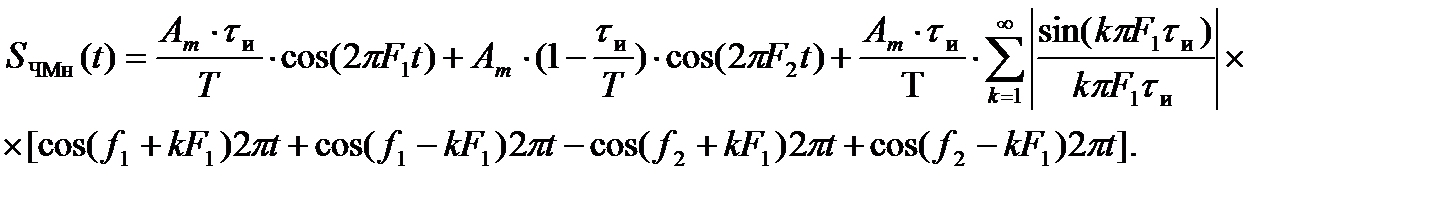(10.3)

Первое слагаемое определяет составляющую на частоте f₁ , второе - на частоте f₂ . Формирование ЧМн сигнала с разрывом фазы показано на рис. 10.5.

Из рис. 10.5 видно, что ширина спектра ЧМн сигнала отличается от спектра сигнала АМн на величину 2∆f_m: ΔF_ЧМн = 2kF₁ + 2∆f_m, где k – номер учитываемой гармоники.

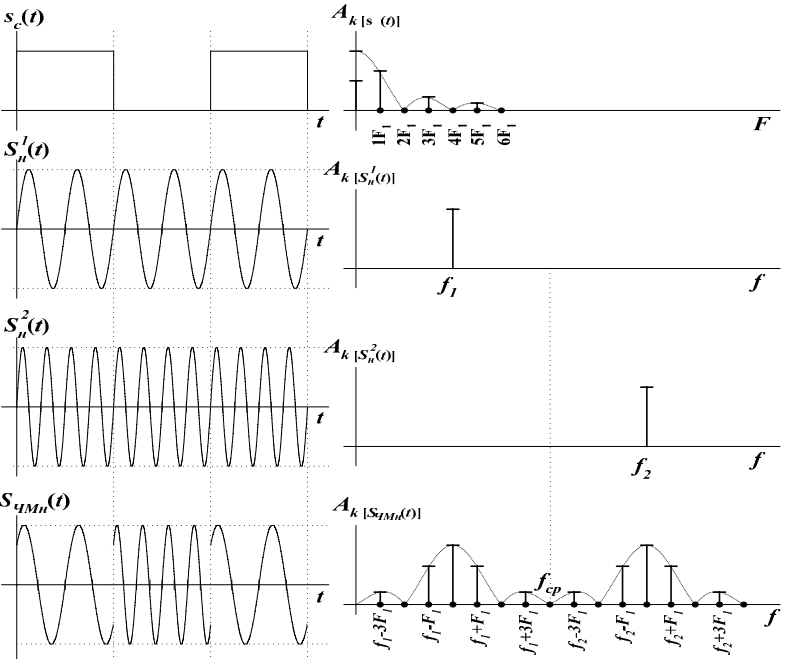
Рис. 10.5. Временные и спектральные характеристики формирования ЧМн сигнала с разрывом фазы

Например, при необходимости передать цифровой сигнал со скоростью V = 75 бит/с, ∆f_m = 250 Гц, k = 3, ширина спектра

ΔF_ЧМн = 2∙3∙(75/2)+2∙250 = 725 Гц.

Общий вид ЧМн сигнала без разрыва фазы (рис. 10.6) можно записать в виде [5]: S_ЧМн(t) = A_mcos[ω_нt + ∆φ(t)], где ∆φ(t) – приращение фазы, обусловленное приращением частоты ∆ω(t).

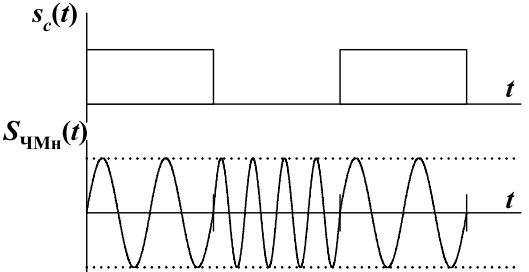
Рис. 10.6. Временные характеристики формирования ЧМн колебаний без разрыва фазы

Этот вид манипуляции предполагает использование одного источника колебаний (рис. 10.7), частота которого изменяется посредством управляемой реактивности (в этом случае фаза изменяется непрерывно – без разрыва).

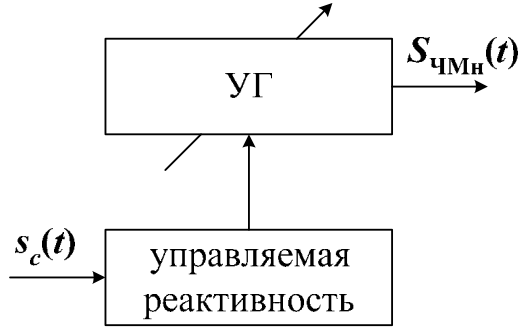
Рис. 10.7. Структурная схема формирования ЧМн колебаний без разрыва фазы

Спектральный состав ЧМн сигнала без разрыва фазы можно получить, раскрывая выражение для S_ЧМн(t):

.

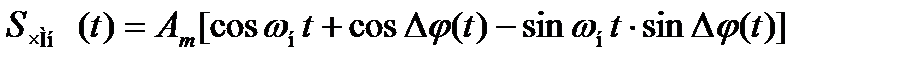Из этой формулы следует, что для нахождения спектра ЧМн сигнала необходимо определить спектр функций cosΔφ(t) и sin Δφ(t) разложив их в ряд Фурье:

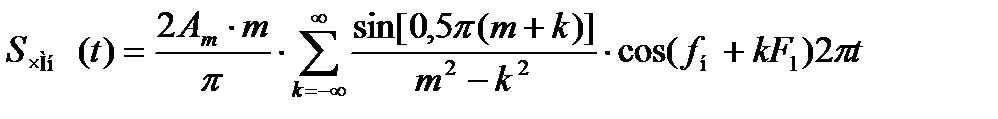. (10.4)

Из спектральной характеристики (10.4) видно, что для спектра при m_ЧМн << 1 энергия колебания находится вблизи f_н. Спектр ограничен несущей и двумя боковыми частотами, а ширина спектра равна ширине спектра АМн сигнала [2, 5]:

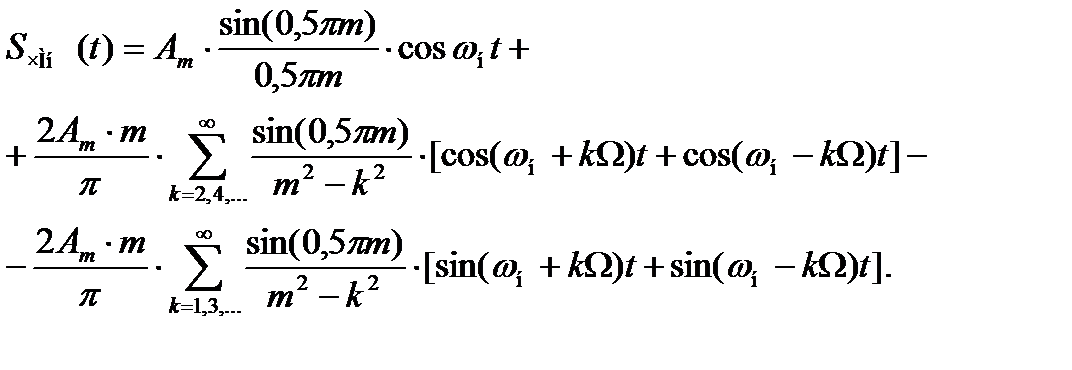(10.5)

По мере увеличения индекса частотной модуляции энергия концентрируется вблизи частот f₁ и f₂. На рис. 10.8 приведены спектры колебаний при различных m_ЧМн.

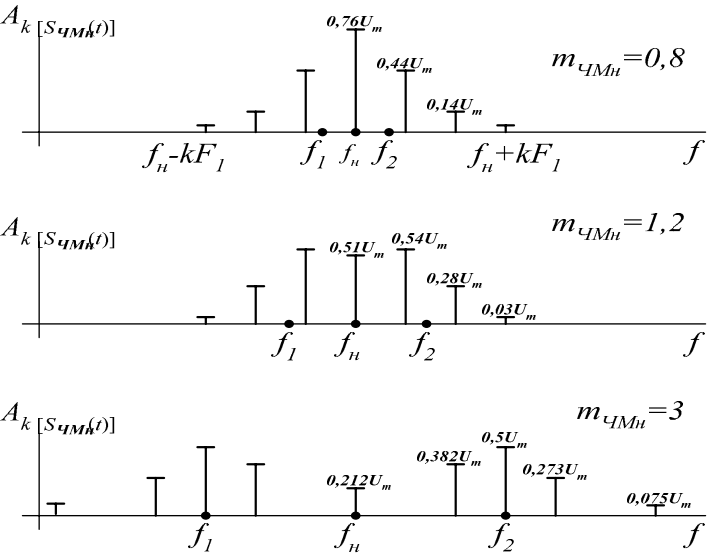
Рис. 10.8. Спектральные характеристики ЧMн сигнала без разрыва фазы для различных индексов модуляции

Ширина спектра определяется по общей формуле [2, 5]:

ΔF_ЧМн = 2(∆f_m + ∆F) = 2F(m – 2) = 2∆f_m(1 + 2/m), (10.6)

либо по формулам для различных m_ЧМн:

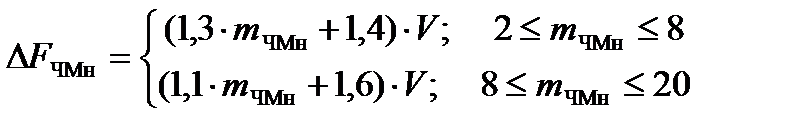(10.7)

где V – скорость телеграфирования в бодах.