Спектр сигналов угловой модуляции

Сигналы с угловой модуляцией, как и при AM, могут быть представлены в виде суммы гармонических колебаний. Сравнительно просто это можно сделать для тональной модуляции. При тональной модуляции спектры ФМ и ЧМ одинаковы, если m_ФМ = m_ЧМ = m, поэтому будем рассматривать только спектр ЧМ сигнала.

Преобразуем (9.8) по формуле косинуса суммы двух аргументов:

S_ЧМ(t) = U_m∙cos(ω₀t + m∙ sinΩt) = U_m∙cos(ω₀t)∙cos(m∙ sinΩt) -

- U_m∙sin(ω₀t)∙sin(m∙ sinΩt). (9.9)

Из теории бесселевых функций [2] известны следующие соотношения:

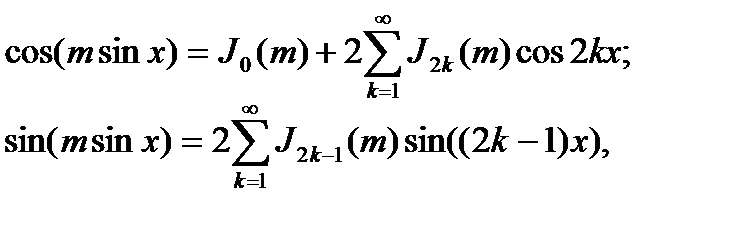(9.10)

где J_k(m) – функция Бесселя k -го порядка от аргумента m. Подставляя (9.10) в (9.9), выполняя обычные алгебраические преобразования и раскрывая произведение тригонометрических функций, получаем:

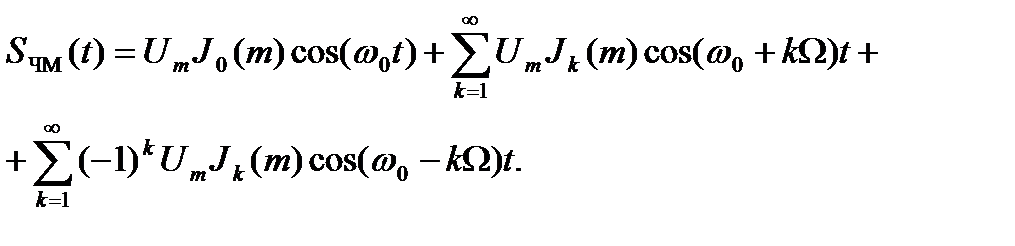(9.11)

Таким образом, спектр даже для однотональной угловой модуляции является довольно сложным. В формуле (9.11) первый член – гармоническая составляющая с частотой несущей. Группа гармонических составляющих с частотами (ω₀ + kΩ), k = 1, 2, …, определяет верхнюю боковую полосу частот, а группа составляющих с частотами (ω₀ - kΩ), k = 1, 2, …, нижнюю боковую полосу частот.

Число верхних и нижних гармоник боковых частот теоретически бесконечно.

Боковые гармонические колебания расположены симметрично относительно ω₀ на расстоянии Ω. Амплитуды всех компонент спектра, в том числе и с частотой ω₀, пропорциональны значениям функций Бесселя J_k(m).

Формулу (9.11) можно представить в более компактном виде. Действительно учитывая (-1)^k J_k(m) = J_k(m), получаем:

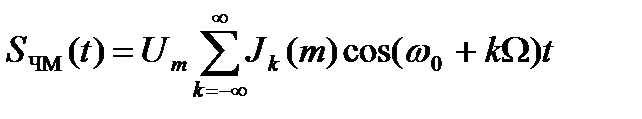. (9.12)

Для построения спектральных диаграмм необходимо знание функций Бесселя J_k(m) при различных значениях k и m. Эти сведения имеются в математических справочниках [3]. На рис. 9.3 приведены графики функций Бесселя при k = 0, 1, 2, …, 7. Значения функций Бесселя, отсутствующих на графиках, можно найти по рекуррентной формуле:

.

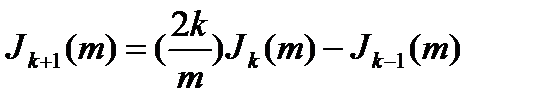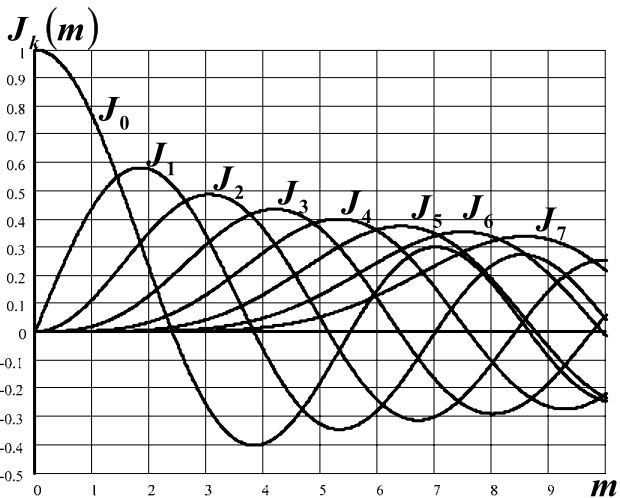
Рис. 9.3. График функций Бесселя

Пример. Задан модулированный сигнал S(t) = 10∙cos(2∙10⁶t + 3∙cos10⁴t). Построить спектральную диаграмму этого сигнала.

Из математического уравнения сигнала следует, что это однотональная угловая модуляция с индексом m = 3. Спектральные составляющие сигнала определяем из уравнения (9.11), приняв k = 0, 1, 2, 3,... , до тех пор, пока амплитуда составляющих не будет заданной, например меньше 2% от U_m. По результатам расчетов построена спектральная диаграмма (рис. 9.4).

Рис. 9.4. Спектральная диаграмма сигналов с однотональной угловой модуляцией при m = 3

Анализ графиков функций Бесселя показывает, чем больше порядок k функции Бесселя, тем при больших аргументах m наблюдается ее максимум, однако при k > m значения функций Бесселя оказываются малой величиной. Следовательно, малыми будут и соответствующие составляющие спектра; ими можно пренебречь. Поэтому ширину спектра сигналов с угловой модуляцией можно приближенно определить по формуле:

Δω_УМ ≈ 2(m + 1)Ω, (9.13)

где Ω – частота модулирующего сигнала. Для передачи модулированного сигнала с высокой точностью иногда считают, что надо учитывать спектральные составляющие с уровнем не менее 1% от уровня несущей. Тогда ширина спектра с угловой модуляцией Δω_УМ ≈ 2(m + m^1/2 + 1)Ω [21, 32, 39].

Если m < 0,6, то ширина спектра угловой модуляции соизмерима с шириной спектра амплитудной модуляции. Если m >> 1 то при угловой модуляция из (9.13) и (9.7) следует, что ширина полосы частот примерно равна удвоенной девиации частоты.