Колебательное движение МТ в поле силы тяжести, в среде с сопротивлением под действием возмущающей силы

МТ массы m (рис. 10), подвешенная к пружине с коэффициентом жесткости с, находится в среде с сопротивлением, пропорциональным первой степени скорости, и на нее действует вертикальная гармоническая возмущающая сила. Найти уравнение движения МТ, если известны ее начальное положение – координата х₀ и ее начальная скорость – V₀, направленная по вертикали.

ст

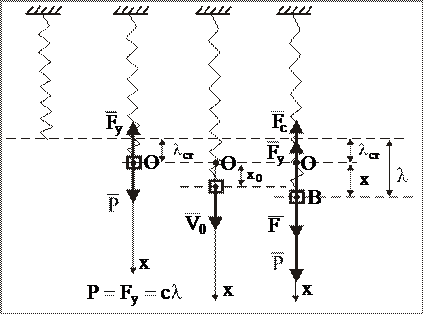
Рис. 10

Пусть F_у = –сl – сила упругости пружины (восстанавли-вающая сила), где l – удлинение пружины;

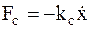– сила сопротивления среды, где 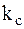– постоянный коэффициент сопротивления среды;

F = H sin pt – возмущающая сила, где Н – амплитуда (наибольшее значение), а р – угловая частота возмущающей силы.

Ось х направлена вертикально вниз, а начало координат (точка О) выбрано в положении статического равновесия, для которого .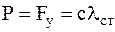

Силовая схема изображена на рис. 10.

Составим уравнение движения:

.

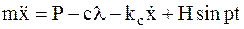Учтя, что 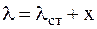, P=cl_ст, дифференциальное уравнение колебательного движения МТ примет вид:

.

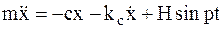Приведя это уравнение к каноническому виду, получим:

.

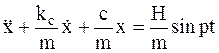Используем уже введенные обозначения

.

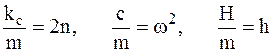Тогда дифференциальное уравнение движения примет вид:

.

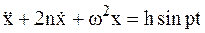Это линейное, неоднородное дифференциальное уравнение второго порядка, решения которого в общем и различных частных случаях представлены в пунктах 1.5.1 – 1.5.5.

Примечания.

Если колебательное движение МТ происходит на наклонной плоскости, то ось х направляется вдоль этой плоскости и все силы, действующие на МТ, проектируются на эту ось.

Если плоскость горизонтальна, то задача упрощается, так как l_ст и проекция силы тяжести Р на ось х будут равны нулю.

Если МТ подвешена к нескольким пружинам разной жесткости, соединенных последовательно или параллельно, то эти пружины заменяются одной им эквивалентной пружиной.