ІІ.5.3. Комбинаторика крестовых клеточных структур
Результаты последовательных ите-раций исходной квадратной клетки мо-жно представить элементами комбина-торных композиций, плотно упаковы-вающих плоскость.
Исходная квадратная клетка в ком-бинаторном соединении покрывает плоскость непрерывной сетью квадра-тов с тождественно расположенными сторонами.
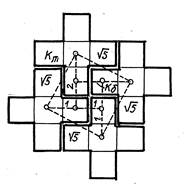
5-клеточные кресты плотно упако-вывают плоскость, примыкая друг к другу по свастикообразным швам. Ко-личественной характеристикой их вза-имного расположения можно принять отношения катетов прямоугольных тре-угольников, гипотенузы которых со-единяют центры этих крестов. В дан-ном случае эти треугольники являются половинами двойных квадратов с отно-шением малых катетов Кm к большим Кb как 1 к 2. При этом подкоренное значе-ние длины гипотенузы (5) равно числу квадратов, слагающих каждый крест (рис.ІІ.39).
|
Рис. ІІ.39. Комбинаторное соединение четырёх пятиклеточных крестов
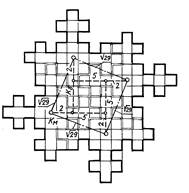
Комбинаторика 4-х 29-клеточных элементов определяет их плотную упа-ковку благодаря замковым соединени-ям. Прямые, соединяющие их центры, являются гипотенузами прямоугольных треугольников с отношением катетов 2 к 5. Комбинаторная композиция этих фигур образует их систему как единое
|
Рис. ІІ.40.Замковое соединение 4-х фигур второй итерации квадрата
|
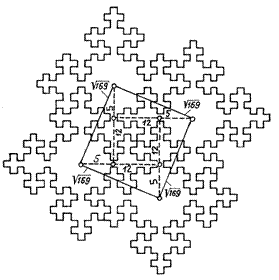
Рис. ІІ.41.Замковое соединение 4-х фигур третьей итерации квадрата
|
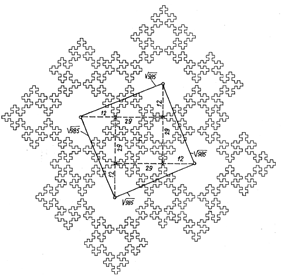
Рис. ІІ.42. Замковое соединение четырёх фігур четвёртой итерации квадрата
целое, структура связей которой опре-деляется их замковыми соединениями
(рис. ІІ.40).
Комбинаторное соединение четы-рёх 169-клеточных фигур в замок обра-зует их систему как единое целое. Прямые, соединяющие центры этих фигур, являются гипотенузами прямо-угольных треугольников, малые катеты которых относятся к большим как 5 к 12. Сумма их квадратов (25 и 144) равна квадрату гипотенузы (169), в свою очередь, численно равному коли-честву клеток в каждой из соединяемых фигур (рис. ІІ. 41).
Комбинаторное сое-динение четырёх 985-клеточных фигур в за-мок образуют их систе-му как единое целое. Прямые, соединяющие центры этих фигур, яв-ляются гипотенузами прямоугольных треуго-льников, малые катеты которых относятся к бо-льшим как 12 к 29. Сум-ма их квадратов (144 и 841) равна квадрату ги-потенузы (985),в свою очередь, численно рав-ному количеству клеток в каждой из соединя-емых фигур (рис. ІІ. 42).
Следуя принятой методике преобразо-вания фигур предыду-щих итераций в по-следующие, можно получать всё более сложные по своей геометрической стру-ктуре фигуры после-дующих итераций, ра-сширящихся до беско-нечно больших разме-ров.
Сравнительная оценка изменения от-ношений катетов в треугольниках, гипо-тенузы которых соединяют центры этих фигур, позволяет определить количе-ственный закон протекания всего ите-рационного процесса.( см.табл. 1).
Таблица 1
| № итера- ции – (n) | I | II | III | IV | V | VI | VII |
| kb катет ольшой | |||||||
| km – катет малый | |||||||
| Число клеток | |||||||
| Число сторон |
Анализ таблицы указывает на сле-дующую закономерность:
kb(n) = 2kb(n-1) + km (n – 1).
Поскольку km(n-1) = kb(n-2), то тогда
kb(n) = 2kb(n-1) + kb (n-2),
откуда возникает новый числовой ряд
вида:
| an = 2an-1 + an-2 |
Это выражение является рекур-рентной формулой итерационного про-цесса расширения квадрата.
Числовой ряд, определяющий ха-рактер изменения количества клеток в фигурах последовательных итераций, начиная с третьей, выражается следу-ющей зависимостью:
| an = 6an-1 – an-2 |
Особенности изменения количест-
ва сторон последовательных резуль-таттов итераций, начиная с 3-ей, опи-сывается следующим выражением:
| an = 4 аn-1+ аn-2 |
Эти три числовых ряда определя-
ют соответственно качественные и ко-
личественные характеристики дина-
мических процесов роста объектов жи-
вой и неживой природы, имеющих кле-
точное строение.
Дата добавления: 2016-06-05; просмотров: 1861;











