Рассуждения по этому поводу

Ответом на этот вопрос является сентенция «…то есть, фракталы на ма-лых масштабах выглядят в среднем так же, как и на больших» [7].

Очевидно, в понятие «фрактально-го» масштаба вкладывается смысл, от-личный от традиционного. Общеприня-то считать, что масштабом изображе-ния является численное значение отно-шения линейных размеров изображе-ния к линейным размерам изображен-ного объекта. В свою очередь, линей-ным размером чего бы то ни было яв-ляется отношение длины натуральной единицы измерения (мм, см, м) или единицы натурального масштаба к дли-не измеряемого отрезка.

Понятие «масштаб» неразрывно связано с понятиями «изображение» и «изображаемый объект» (в традицион-ном понимании). Фрактал, как изобра-жаемый объект, в природе не сущест-вует. Там существуют природные объ-екты, имеющие фрактальную структуру. А фрактал, как изображение, сущест-вует. Но его линейные размеры не с чем сравнивать, (если понимать его как единое целое), так как не существует натуры, структура которой изоморфна структуре этого изображения. Отсюда следует, что изображение фрактала, как единое целое является системой взаимосвязанных частей, самоподобие которых определяется изменением ко-эффициента С в рекуррентном уравне-нии Z® Z ² – C нелинейногоитераци-онного процесса. Тогда исчезает поня-тие единицы натурального масштаба. Но, так как понятие масштаба, неотъ-емлемое от понятия самоподобия оста-ётся, то в качестве единицы измерения частей фрактала можно принять, до-пустим, его инициатор. Тогда, участвуя в конструктивном процессе итераций этого инициатора, отношение его раз-

мера к размеру связанного с ним гене-ратора сохраняется и поэтому «внут-ренний масштаб» фрагментов фракта-ла есть величина постоянная, опреде-ляемая отношением размеров инициа-тора и генератора. Но, если таким об-разом возникло понятие внутреннего масштаба как постоянной величины, то, очевидно, что для сравнительной оцен-ки различных по своим размерам физи-чески двумерных фрактальных фраг-ментов следует их отнести к системе двух взаимно-перпендикулярных осей декартовых координат, совмещенных с рамкой изображения. (рис.ІІ.31) Тогда самоподобные фрагменты приобретут название закономерно уменьшающихся в стремлении к дробномерному преде-лу или наоборот, закономерно увеличи-вающихся при обратном направлении итерации. В сравнении друг с другом, они будут характеризоваться словами «бо¢льший», «ме¢ньший». Внешне эта ситуация похожа на перспективу стол-бов вдоль дороги, изображения кото-рых закономерно уменьшаются, стре-мясь к нульмерному пределу в виде точки схода по принципу перспе-ктивных сокращений:«дальше – мень-ше, ближе – больше» ( рис. ІІ.32).

Так как все линейные фракталы практически придуманы их авторами, то нетрудно пополнять их галерею но-выми по их образу и подобию (рис.ІІ.32) или их вариантами (рис. ІІ.29, ІІ.30). К числу варианта «дракона» относится результат итераций генератора как ра-вностороннего прямого угла, образую-щего стороны равнобедренного треу-гольника, основанием которого высту-пает исходный прямолинейный иници-атор (рис. ІІ.29), роль котрого в после-дующих итерациях играют уменьшаю-щиеся стороны генератора. В итоге по-лучается фрактальный «дракон», само-подобно сжимающийся и закономерно усложняющий свою структуру (рис.ІІ.30)

Если вернуться к линейным фрак- талам типа «дракона» Хартера-Хейту-эя (рис. ІІ.7), «колбасы» Миньковского (рис. ІІ.14), и «отеля» Гильберта (рис. ІІ.15), элементы которых не самоподоб-

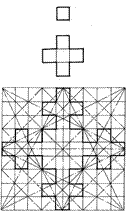
Рис. ІІ.33.2 итерациифрактального расширения квадрата

Рис. ІІ.34.Результат третьей

итерации квадрата

Рис. ІІ.35. Результат4-й итерации квадрата (снежинка Ткача-Нифанина)

ны, а конгруэнтны, то их внешний мас-штаб будет совпадать с внутренним и будет величиной постоянной.

Отсюда вариант ответа на 3-й воп-рос:так как изменения размеров частей фрактального изображения как целого определяются изменением параметра С в рекуррентной формуле итерационного процесса, то их вну-тренний масштаб есть величина по-стоянная, а количественная мера их изменения определяется результата-ми их отнесения к внешней системе отсчета.

Общие выводы из рассуждений:

1.Так как наука о фракталах на-зывается фрактальной геометрией,

то она должна иметь все признаки фундаментальной геометрической науки: однозначное определение, ак-сиоматику, предмет и метод иссле-дования этого предмета.

2. По своей природе фракталы являются графо-аналитическими мо-делями динамических процессов, опи-сываемых соответствующими рекур-рентными уравнениями их итераци-онных преобразований.

3.Так как фракталы это изо-бражения, то они, как своеобразные графики и диаграммы тех динами-ческих процессов, которые описыва-ются соответствующими аналити-ческими зависимостями, обладают изобразительными свойствами, коди-рующими информа-цию о количествен-ных и качественных характеристиках этих процессов. Изу-чение этих свойств должно быть предме-том исследования фрактальной геоме-трии как фундамен-тальной науки.