Рассуждения по этому поводу.

Если следовать логике авторского определения фрактала, то «целым» должно быть то, что состоит из «час-тей», т.е., та дробномерная фракталь-ная композиция, которая получается в результате бесконечного количества итераций, подобно преобразующих исходную, довольно простую геометри-ческую фигуру инициатора. Преобразование подобия является разновидностью гомологии при не-собственной оси и собственном центре подобия. Так как таких преобразований бесчисленное множество, то, очевидно, они должны объединяться в группу по-добных преобразований, имеющую свои инварианты, в том числе и графи-ческие. Очевидно, они кодируются про-граммами итерирования, так как части подобны друг другу, но никак не подоб-ны целому. Если во фрактале «сне-жинка Коха» целым считать фигуру са-мой снежинки, то его четырехзвенные самоподобные части-генераторы никак не подобны её «бесконечнозвенной» фигуре. Если считать целым прямоли-нейный инициатор, то он не может состоять из множества ломаных само-подобных генераторов, не образующих фигуру снежинки. Получается парадо-кс, ибо «что присуще целому…, то не присуще части целого, но чтобы поз-нать целое, надо изучить его составные части» [56].

Редким исключением среди рас-смотренных линейных фракталов, у ко-торых чести подобны целому, является «золотая звезда» И.Тугого при условии, что роль «целого» играет центральная пентаграмма или инициатор преобра-зования.

Особое внимание следует обратить на структуру таких фракталов, как «дра-кон» Хартера-Хейтуэя, «колбасу» Минь-ковского и «отель» Гильберта, получа-емых итерациями сдвига, а не подобия.

В итоге полученные фигуры фракталов состоят не из самоподобных, а из кон-груэнтных фигур одного или нескольких типоразмеров. Таким образом, эти и по-добные им «фракталы» не подходят под определение Б. Мандельброта. Впрочем, если считать преобразование сдвига разновидностью подобия с не-собственными центром и осью, то они условно подходят под это определение.

Отсюда возможный ответ на 2-й вопрос: Так как у большинства рас-смотренных фраталов части подоб-

ны друг другу, но не подобны их сово-

Рис. ІІ.31.Отнесение элементов фрактальной картины к внешней системе отсчета

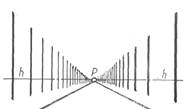
Рис. ІІ.32. Перспективне сокращения как пример самоподобия