Смысл понятия rota.

В научной и технической литературе часто «завихренность » векторного поля связывают с наличием замкнутых самих на себя векторных линий. Это не совсем точно. Завихренность поля - понятие локальное, т. е. отнесенное к малой окрестности рассматриваемой точки пространства. Завихренность поля имеет место, если в рассматриваемой точке пространства .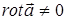

Представим себе бесконечную в обе стороны прямолинейную вихревую нить интенсивности Г. Величина Г определена условием

.

Г

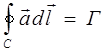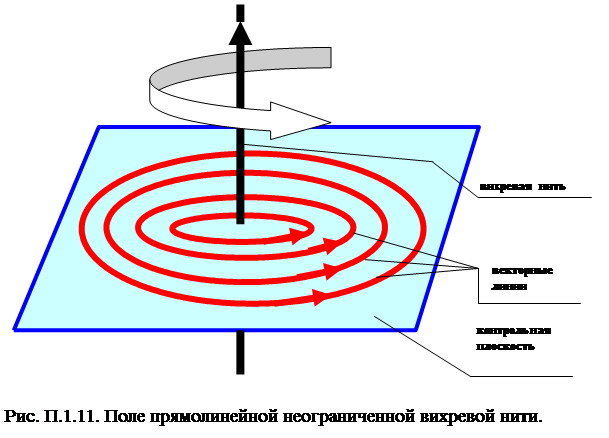
В условиях осевой симметрии модуль вектора 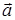можно рассчитать по соотношению

,

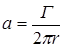где r – расстояние от вихревой нити до точки наблюдения. Величина 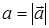убывает обратно пропорционально расстоянию r, последнее означает, что число проводимых векторных линий на единицу длины в плоскости, перпендикулярной вихревой нити, должно убывать по этому же закону. Заметим, что во всем пространстве 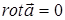, за исключением точек вихревой нити. Интересна особенность графического представления векторных линий: замкнутые векторные линии есть, а завихренности поля вне вихревой нити нет.

Теперь рассмотрим «вихревую трубку» - совокупность всех вихревых линий, пронизывающих конечную область S, ограниченную замкнутым контуром С. Пусть для простоты все вихревые нити являются бесконечными в обе стороны и прямолинейными, параллельными друг другу, а область S – представляет собой круг радиуса r₀, контур С – окружность с центром в начале координат, плоскость, в которой лежит S, перпендикулярна вихревым нитям.

Пусть по сечению вихревой трубки выполнено условие dГ=g2prdr для распределенной равномерно по поверхности интенсивности вихреисточника g, причем условие g=const принято для облегчения расчетов. В области r < r₀ имеем Г(r)= gpr², 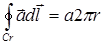,в итоге получаем зависимость a=(1/2)gr

Если мы попытаемся изобразить графически картину проводимых векторных линий на плоскости S, то получим (рис.П.1.12).

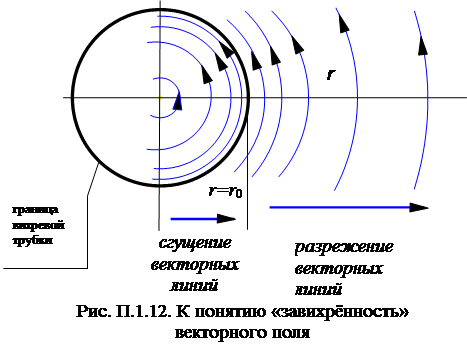
Закономерность расположения проводимых векторных линий вне области, где имеются вихревые линии, аналогична закономерности расположения проводимых векторных линий в окрестности отдельной вихревой нити (в области r>r₀ имеет место «разрежение» силовых линий), а в области r < r₀ мы с ростом r наблюдаем «сгущение» проводимых векторных линий. Изменение характера расположения замкнутых проводимых векторных линий свидетельствует о том, что в рассматриваемой области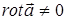

Если в соответствии с соотношением (8) раздела П.1.7 вычислить модуль вектора rot 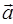в окрестности начала координат

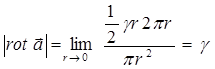, (r<r₀),

то легко видеть, что модуль 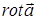равняется поверхностной плотности интенсивности вихреисточника. Можно говорить, что 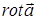определяет локальную количественнуюмерузавихрённости векторного поля и направление локальной оси, задающей плоскость максимальной циркуляции векторного поля в окрестности рассматриваемой оси. В заключение отметим, что примеры графических построений в настоящем разделе служат иллюстративным целям, реальные структуры вихревых полей могут быть значительно более сложными, поэтому вычисление, а также выяснение физического смысла той или иной дифференциальной операции необходимо производить, исходя из соответствующих математических определений.