Расчёт цепей с взаимосвязанными катушками индуктивности.

При рассмотрении цепей синусоидального тока до сих пор учитывалось только явле­ние самоиндукции катушек, обусловлен­ное током в цепи. Цепи, в которых наво­дятся ЭДС между двумя (и более) взаимно связанными катушками, называются индуктивно связанными цепями.Рассмот­рим явление возникновения ЭДС в одном из контуров при изменении тока в другом.

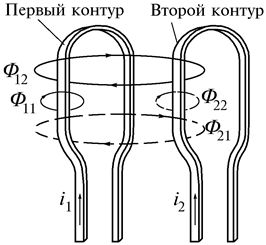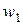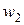Контуры (рис. 2.19) представляют собой плоские тонкие катушки с числами витков и . Поток самоиндукции 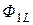, созданный то­ком 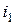, может быть представлен в виде потока рассеяния 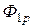, пронизывающего только пер­вый контур, и потока 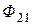, пронизывающего второй контур

= + .

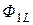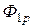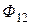Аналогично определяем поток самоиндукции второго контура

= + .

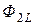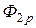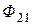Поток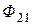и и 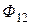называют потоками взаимной индукции. Их принято обо­значать двумя индексами: первый индекс указывает, с каким контуром сцепляется поток, второй – номер тока, вызвавшего данный поток. Например, поток 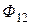вы­зван током 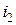, сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры

= ± ; = ± ,

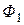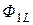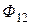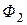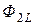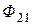где «+» соответствует согласному направлению потоков, «–» – встречному на­правлению.

Полные потокосцепления первого и второго контуров

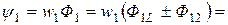
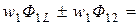
(2.48)

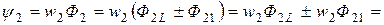
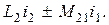(2.49)

Отношение потокосцепления взаимной индукции в одной цепи к току в дру­гой называется взаимной индуктивностью

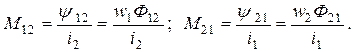
Для линейных электрических цепей всегда выполняется равенство

.

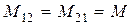Взаимная индуктивность двух катушек зависит от числа витков, геометри­ческих размеров магнитопровода и взаимного расположения катушек, а также от абсолютной магнитной проницаемости среды (материала магнитопровода). Ин­дуктивную связь двух катушек характеризуют коэффициентом связи

.

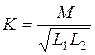Этот коэффициент всегда меньше единицы, так как магнитный поток взаим­ной индукции всегда меньше потока самоиндукции и может быть увеличен за счет уменьшения потоков рассеяния бифилярной намоткой катушек (двойным проводом) или применением для магнитопровода материала с высокой абсолют­ной магнитной проницаемостью.

ЭДС самоиндукции

Если по проводнику протекает переменный ток, то вокруг этого проводника он создает переменный магнитный поток, который создает переменное потокосцепление, а нон в свою очередь порождает ЭДС.

Таким образом, ЭДС каждой катушки определяется алгебраической суммой ЭДС самоиндукции и взаимной индукции. Для определения знака ЭДС взаимной индукции размечают зажимы индуктивно связанных элементов цепи. Два зажима называют одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции складыва­ются. Такие выводы обозначают на схемах одинаковыми условными значками, например, точками или звездочками (рис. 2.20 а, б). 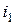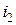Одинаково направленные токи и (рис. 2.20 а) относительно зажимов 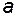и 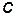вызывают совпадающие по направлению потоки самоиндукции 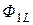( 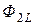) и взаимной индукции 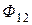( 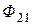). Следовательно, зажимы 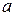и 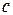являются одноименными. 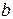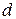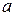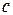Одноименной является и другая пара зажимов и , но условными значками обозначают только одну пару одноимен­ных выводов, например, и (рис. 2.20 а). Если токи и направ­лены неодинаково относительно одноименных зажимов (рис. 2.20 б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.

На схемах магнитопроводы, как правило, не показывают и ограничиваются только обозначением одноименных зажимов (рис. 2.20 в, г).

Одноименные зажимы можно определить опытным путем. Для этого одну из катушек включают в цепь источника постоянного тока, а к другой присоеди­няют вольтметр постоянного тока. Если в момент подключения ис­точника стрелка измерительного прибора отклоняется, то зажимы индуктивно связанных

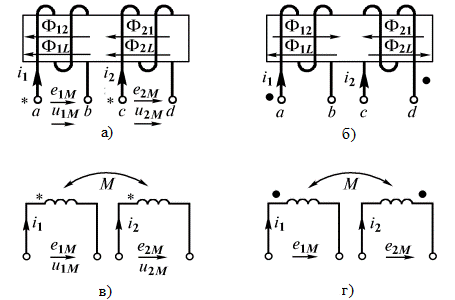
Рис. 2.20

катушек, подключенные к положительному полюсу источника и поло­житель­ному зажиму измерительного прибора, являются одноименными.

Определим знаки ЭДС и напряжения взаимной индукции. Допустим, пер­вая катушка (рис. 2.20 а) разомкнута, а во второй протекает ток . Выберем поло­жительные направления для 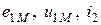одинаковыми относительно одноимен­ных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда 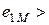0, потенциал зажима b больше потенциала зажима а, следовательно, 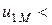0.

По правилу Ленца знаки 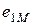и 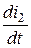всегда противоположны, поэтому

.

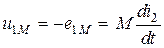В комплексной форме уравннеие имеет вид

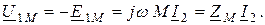(2.50)

При встречном включении катушек (рис. 2.20 б)

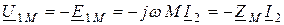. (2.51)

Из (2.50) и (2.51) видно, что вектор напряжения на взаимной индуктивности 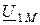сдвинут по фазе относительно вектора тока 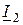на угол ±90°.

Сопротивление 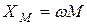называется сопротивлением взаимной индуктивно­сти, а 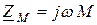– комплексным сопротивлением взаимной индуктивно­сти.

Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».