Расчёт методом применения закона Кирхгофа.

1. Определяем кол-во узлов и ветвей.

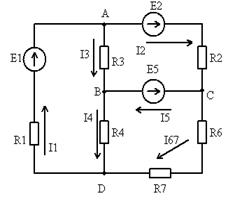
1. Произвольно зададим направление токов всех ветвей.
2. Составляем уравнение по первому закону Кирхгофа для каждого независимого узла: k-1=3.

Для точки А: I₁-I₃-I₂=0

Для точки В: I₃+I₅-I₄=0

Для точки D: I₄-I₁+I₆₇=0

1. Недостающие уравнения: m-(k-1)=3 составляем по второму закону Кирхгофа для каждого независимого контура:

E₁=I₃R₃+I₄R₄+I₁R₁

E₂-E₅= -I₃R₃+I₂R₂+I₅*0

E₅= I₆₇(R₆+R₇)-I₄R₄

1. Решая систему уравнений находим неизвестные токи в ветвях.
2. По результатам полученных численно значений токов выполняем действия:

1). Уточняем направление тока в ветвях: если ток отрицательный, то пишем примечание – реальное направление тока противоположено показанному на схеме.

2). Определяем режим работы источника питания: если направление ЭДС и реального тока совпадают, то режим источника питания – режим генератора, если направление ЭДС и реального тока противоположно, то это режим потребителя.

7. Проверка решения – проверка уравнения баланса мощностей: алгебраическая сумма мощностей источников равна арифметической сумме мощностей нагрузок

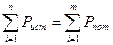
Если направление ЭДС и реального тока совпадают, то Р_ист=EI (>0), если направление ЭДС и реального тока не совпадают, то Р_ист= -EI (<0).

Можность нагрузки Р_потр=I_n²R_n

Итак, уравнение баланса мощностей для нашей схемы:

E₁I₁+E₂I₂-E₅I₅=I₁²R₁+I₂²R₂+I₃²R₃+I²₄R₄+I²₆₇(R₆+R₇)

Итак, если поле подстановки численных значений величин уравнения баланса обращается в тождество, то задача решена верно.

Достоинство метода: Его простота.

Недостатки метода:Большое количество совместно решаемых уравнений для сильно разветвленных цепей.

Поэтому метод применяется для расчета сложных цепей на компьютерах, в ручную не рекомендуется.